fairmodels: a Flexible Tool for Bias Detection, Visualization, and Mitigation in Binary Classification Models

Jakub Wiśniewski; Przemysław Biecek

doi:10.32614/RJ-2022-019

Introduction

Responsible machine learning and, in particular, fairness is gaining attention within the machine learning community. This is because predictive algorithms are becoming more and more decisive and influential in our lives. This impact could be less or more significant in areas ranging from user feeds on social platforms, displayed ads, and recommendations at an online store to loan decisions, social scoring, and facial recognition systems used by police and authorities. Sometimes it leads to automated systems that learn some undesired bias preserved in data for some historical reason. Whether seeking a job (Lahoti et al. 2019) or having one’s data processed by court systems (Angwin et al. 2016), sensitive attributes such as sex, race, religion, ethnicity, etc., might play a significant role in the decision. Even if such variables are not directly included in the model, they are often captured by proxy variables such as zip code (a proxy for the race and wealth), purchased products (a proxy for gender and age), eye colour (a proxy for ethnicity). As one would expect, they can give an unfair advantage to a privileged group. Discrimination takes the form of more favorable predictions or higher accuracy for a privileged group. For example, some popular commercial gender classifiers were found to perform the worst on darker females (Buolamwini and Gebru 2018). From now on, such unfair and harmful decisions towards people with specific sensitive attributes will be called biased.

The list of protected attributes may depend on the region and domain for which the model is built. For example, the European Union law is summarized in the Handbook on European non-discrimination law European Union Agency for Fundamental Rights and Council of Europe (2018), which lists the following protected attributes that cannot be the basis for inferior treatment: sex, gender identity, sexual orientation, disability, age, race, ethnicity, nationality or national origin, religion or belief, social origin, birth, and property, language, political or other opinions. This list, though long, does not include all potentially relevant items, e.g. in the USA, a protected attribute is also pregnancy, the status of a war veteran, or genetic information.

While there are historical and economic reasons for this to happen, such decisions are unacceptable in society, where nobody should have an unfair advantage. The problem is not simple, especially when the only criterion set for the system is performance. We observe a trade-off between accuracy and fairness in some cases where lower discrimination leads to lower performance (Kamiran and Calders 2011). Sometimes labels, which are considered ground truth, might also be biased (Wick et al. 2019), and when controlling for that bias, the performance and fairness might improve simultaneously. However fairness is not a concept that a single number can summarize, so most of the time, when we want to improve fairness from one perspective, it becomes worse in another (Barocas et al. 2019).

The bias in machine learning systems has potentially many different sources. Mehrabi et al. (2019) categorized bias into its types like historical bias, where unfairness is already embedded into the data reflecting the world, observer bias, sampling bias, ranking and social biases, and many more. That shows how many dangers are potentially hidden in the data itself. Whether one would like to act on it or not, it is essential to detect bias and make well-informed decisions whose consequences could potentially harm many groups of people. Repercussions of such systems can be unpredictable. As argued by Barocas et al. (2019), machine learning systems can even aggravate the disparities between groups, which is called by the authors’ feedback loops. Sometimes the risk of potential harm resulting from the usage of such systems is high. This was noticed, for example, by the Council of Europe that wrote the set of guidelines where it states that the usage of facial recognition for the sake of determining a person’s sex, age, origin, or even emotions should be mostly prohibited (Council of Europe 2021).

Not every difference in treatment is discrimination. Cirillo et al. (2020) presents examples of desirable and undesirable biases based on the medical domain. For example, in the case of cardiovascular diseases, documented medical knowledge indicates that different treatments are more effective for different genders. So different treatment regimens according to medical knowledge are examples of desirable bias. Later in this paper, we present tools to identify differences between groups defined by some protected attribute but note that this does not automatically mean that there is discrimination.

We would also like to point out that focusing on the machine learning model may not be enough in some cases, and sometimes the design of the data acquisition and/or annotation cause the model to be biased (Barocas et al. 2019).

Assembling predictive models is getting easier nowadays. Packages like h2o (H2O.ai 2017) provide AutoML frameworks where non-experts can train quickly accurate models without deep domain knowledge. Model validation should also be that simple. Yet this is not the case. There are still very few tools to support the fairness diagnostics of the model.

Two main kinds of fairness are a concern to multiple stakeholders. These are group and individual fairness. The first one concerns groups of people with the same protected attributes (gender, race, etc.). It focuses on measuring if these groups are treated similarly by the model. The second one is focused on the individual. It is most intuitively defined as treating similar individuals similarly (Dwork et al. 2012). Both concepts are sometimes considered to conflict with each other, but they don’t need to be if we factor in certain assumptions, such as whether the disparities are due to personal choices or unjust structures (Binns 2020).

Several frameworks have emerged for Python to verify various fairness criteria, the most popular are aif360 (Bellamy et al. 2018), fairlearn (Bird et al. 2020), or aequitas (Saleiro et al. 2018). They have various features for detecting, visualization, and mitigating bias in machine learning models.

For the R language, until recently, the only available tool was the fairness (Kozodoi and V. Varga 2021) package which compares various fairness metrics for specified subgroups. The fairness package is very helpful, but it lacks some features. For example, it does not allow comparing the machine learning models and aggregating fairness metrics to facilitate the visualization. Still, most of all, it does not give a quick verdict on whether a model is fair or not. Package fairadapt aims at removing bias from machine learning models by implementing pre-processing procedure described in Plečko and Meinshausen (2019). Our package tries to combine the detection and mitigation processes. It encourages the user to experiment with the bias, try different mitigation methods and compare results. The package fairmodels not only allows for that comparison between models and multiple exposed groups of people, but it gives direct feedback if the model is fair or not (more on that in the next section). Our package also equips the user with a so-called fairness_object, an object aggregating possibly many models, information about data, and fairness metrics. fairness_object can later be transformed into many other objects that can facilitate the visualization of metrics and models from different perspectives. If a model does not meet fairness criteria, various pre-processing and post-processing bias mitigation algorithms are implemented and ready to use. It aims to be a complete tool for dealing with discriminatory models in a group fairness setting.

In particular, in the following sections, we show how to use this package to address four key questions: How to measure bias? How to detect bias? How to visualize bias? and How to mitigate bias?

It is important to remember that fairness is not a binary concept that can be unambiguously defined, and there is no silver bullet that will make any model fair. The presented tools allow for fairness exploratory analysis, thanks to which we will be able to detect differences in the behavior of the model for different protected groups. But such analysis will not guarantee that all possible fairness problems have been detected. Also, fairness analysis is only one of a wide range of techniques for Explanatory Model Analysis (Biecek and Burzykowski 2021). Like other explanatory tools, it should be used with caution and awareness.

Measuring and detecting bias

In model fairness analysis, a distinction is often made between group fairness and individual fairness analysis. The former is defined by the equality of certain statistics determined on protected subgroups, and we focus on this approach in this section. We write more about the latter later in this paper.

Fairness metrics

Machine learning models, just like human-based decisions, can be biased against observations related to people with certain sensitive attributes, which are also called protected groups. This is because they consist of subgroups - people who share the same sensitive attribute, like gender, race, or other features.

To address this problem, we need first to introduce fairness criteria. Following Barocas et al. (2019), we will present these criteria based on the following notation.

Let $A \in \{a,b, ...\}$ mean protected group and values $A \neq a$ denote membership to unprivileged subgroups while $A = a$ membership to privileged subgroup. To simplify the notation, we will treat this as a binary variable (so $A = b$ will denote membership to unprivileged subgroup), but all results hold if $A$ has a larger number of groups.
Let $Y \in \{0,1\}$ be a binary label (binary target = binary classification) where $1$ is preferred, favorable outcome.
Let $R \in [0,1]$ be a probabilistic response of the model, and $\hat{Y} \in \{0,1\}$ is the binarised model response, so $\hat{Y} = 1$ when $R \geq 0.5$, otherwise $\hat{Y} = 0$.

Figure 1 summarizes possible situations for the subgroup $A=a$. We can draw up the same table for each of the subgroups.

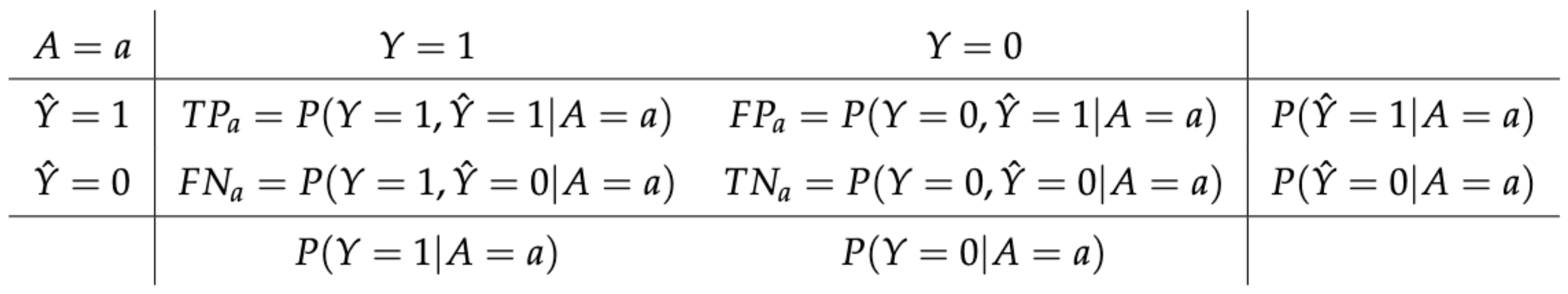
Figure 1: Summary of possible model outcomes for subpopulation $A = a$. We assume that outcome $Y = 1$ is favourable.

According to Barocas et al. (2019) most discrimination criteria can be derived as tests that validate the following probabilistic definitions:

Independence, i.e. $R \perp A$,
Separation, i.e. $R \perp A \mid Y$,
Sufficiency, i.e. $Y \perp A \mid R$.

Those criteria and their relaxations might be expressed via different metrics based on a confusion matrix for a certain subgroup. To check if those fairness criteria are addressed, we propose checking five metrics among privileged group (a) and unprivileged group (b):

Statistical parity: $P(\hat{Y} = 1 | A = a) = P(\hat{Y} = 1 | A = b)$. Statistical parity (STP) ensures that fractions of assigned positive labels are the same in subgroups. It is equivalent of Independence (Dwork et al. 2012). In other words, the values in the last column of Figure 1 are the same for each subgroup.
Equal opportunity: $P(\hat{Y} = 1 | A = a, Y = 1) = P(\hat{Y} = 1 | A = b, Y = 1)$. Checks if classifier has equal True Positive Rate (TPR) for each subgroup. In other words, the column normalized values in the second column of Figure 1 are the same for each subgroup. It is a relaxation of Separation (Hardt et al. 2016).
Predictive parity: $P(Y = 1 | A = a, \hat{Y} = 1) = P(Y = 1 | A = b, \hat{Y} = 1)$. Measures if a model has equal Positive Predictive Value (PPV) for each subgroup. In other words, the row normalized values in the second row of Figure 1 are the same for each subgroup. It is relaxation of Sufficiency (Chouldechova 2016).
Predictive equality: $P(\hat{Y} = 1 | A = a, Y = 0) = P(\hat{Y} = 1 | A = b, Y = 0)$. Warrants that classifiers have equal False Positive Rate (FPR) for each subgroup. In other words, the column normalized values in the third column of Figure 1 are the same for each subgroup. It is relaxation of Separation (Corbett-Davies et al. 2017).
(Overall) Accuracy equality: $P(\hat{Y} = Y | A = a) = P(\hat{Y} = Y | A = b)$. Makes sure that models have the same Accuracy (ACC) for each subgroup. (Berk et al. 2017)

The reader should note that if the classifier passes Equal opportunity and Predictive equality, it also passes Equalized Odds (Hardt et al. 2016), which is equivalent to Separation criteria.

Let us illustrate the intuition behind Independence, Separation, and Sufficiency criteria using the well-known example of the COMPAS model for estimating recidivism risk. Fulfilling the Independence criterion means that the rate of sentenced prisoners should be equal in each subpopulation. It can be said that such an approach is fair from society’s perspective.

Fulfilling the Separation criterion means that the fraction of innocents/guilty sentenced should be equal in subgroups. Such an approach is fair from the prisoner’s perspective. The reasoning is the following: “If I am innocent, I should have the same chance of acquittal regardless of sub-population”. This was the expectation presented by the ProPublica Foundation in their study.

Meeting the Sufficiency criterion means that there should be an equal fraction of innocents among the convicted, similarly, for the non-convicted. This approach is fair from the judge’s perspective. The reasoning is the following: “If I convicted someone, he should have the same chance of being innocent regardless of the sub-population”. This approach is presented by the company developing the COMPAS model, Northpointe. Unfortunately, as we have already written, it is not possible to meet all these criteria at the same time.

While defining the metrics above, we assumed only two subgroups. This was done to facilitate notation, but there might be more unprivileged subgroups. A perfectly fair model would pass all criteria for each subgroup (Barocas et al. 2019).

Not all fairness metrics are equally important in all cases. The metrics above aim to give a more holistic view into the fairness of the machine learning model. Practitioners informed in the domain may consider only those metrics that are relevant and beneficial from their point of view. For example, in Kozodoi et al. (2021) in the fair credit scoring use case, the authors concluded that the separation is the most suitable non-discrimination criteria. More general instructions can also be found in European Union Agency for Fundamental Rights (2018), along with examples of protected attributes. Sometimes, however, non-technical solutions to fairness problems might be beneficial. Note that group fairness metrics will discover not all types of unfairness, and the end-user should decide whether a model is acceptable in terms of bias or not.

However tempting it is to think that all the criteria described above can be met at the same time, unfortunately, this is not possible. Barocas et al. (2019) shows that, apart from a few hypothetical situations, no two of {Independence, Separation, Sufficiency} can be fulfilled simultaneously. So we are left balancing between the degree of imbalance of the different criteria or deciding to control only one criterion.

Acceptable amount of bias

It would be hard for any classifier to maintain the same relations between subgroups. That is why some margins around the perfect agreement are needed. To address this issue, we accepted the four-fifths rule (Code of Federal Regulations 1978) as the benchmark for discrimination rate, which states that “A selection rate for any race, sex, or ethnic group which is less than four-fifths ($\frac{4}{5}$) (or eighty percent) of the rate for the group with the highest rate will generally be regarded by the Federal enforcement agencies as evidence of adverse impact[…].” The selection rate is originally represented by statistical parity, but we adopted this rule to define acceptable rates between subgroups for all metrics. There are a few caveats to the preceding citation concerning the size of the sample and the boundary itself. Nevertheless, the four-fifths rule is an excellent guideline to adhere to. In the implementation, this boundary is represented by $\varepsilon$, and it is adjustable by the user, but the default value will be 0.8. This rule is often used, but users should check if the fairness criteria should be set differently in each case.

Let $\varepsilon > 0$ be the acceptable amount of a bias. In this article, we would say that the model is not discriminatory for a particular metric if the ratio between every unprivileged $b, c, ...$ and privileged subgroup $a$ is within $(\varepsilon, \frac{1}{\varepsilon})$. The common choice for the epsilon is 0.8, which corresponds to the four-fifths rule. For example, for the metric Statistical Parity ($STP$), a model would be $\varepsilon$-non-discriminatory for privileged subgroup $a$ if it satisfies.

\[\begin{equation} \forall_{b \in A \setminus \{a\}} \;\; \varepsilon < STP_{ratio} = \frac{STP_b}{STP_a} < \frac{1}{\varepsilon}. \tag{1} \end{equation}\]

Evaluating fairness

The main function in the fairmodels package is fairness_check. It returns fairness_object, which can be visualized or processed by other functions. This will be further explained in the “Structure” section. When calling fairness_check for the first time, the following three arguments are mandatory:

explainer - an object that combines model and data that gives a unified interface for predictions. It is a wrapper over a model created with the DALEX (Biecek 2018) package.
protected - a factor, vector containing sensitive attributes (protected group). It does not need to be binary. Instead, each level denotes a distinct subgroup. The most common examples are gender, race, nationality, etc.
privileged - a character/factor denoting a level in the protected vector which is suspected to be the most privileged one.

Example

In the following example, we are using German Credit Data dataset (Dua and Graff 2017). In the dataset, there is information about people like age, sex, purpose, credit amount, etc. For each person, there is a risk assessed with taking credit, either good or bad. Therefore, it will be a target variable. We will train the model on the whole dataset and then measure fairness metrics to facilitate the notation (as opposed to training and testing on different subsets, which is also possible and advisable).

First, we create a model. Let’s start with logistic regression.

library("fairmodels")
data("german")

lm_model <- glm(Risk~., data = german, family = binomial(link = "logit"))

Then, create a wrapper that unifies the model interface.

library("DALEX")

y_numeric <- as.numeric(german$Risk) -1
explainer_lm <- DALEX::explain(lm_model, data = german[,-1], y = y_numeric)

Now we are ready to calculate and plot the fairness checks. Resulting plot is presented in Figure 2.

fobject <- fairness_check(explainer_lm,
                protected = german$Sex, privileged = "male",
                verbose = FALSE)

plot(fobject)

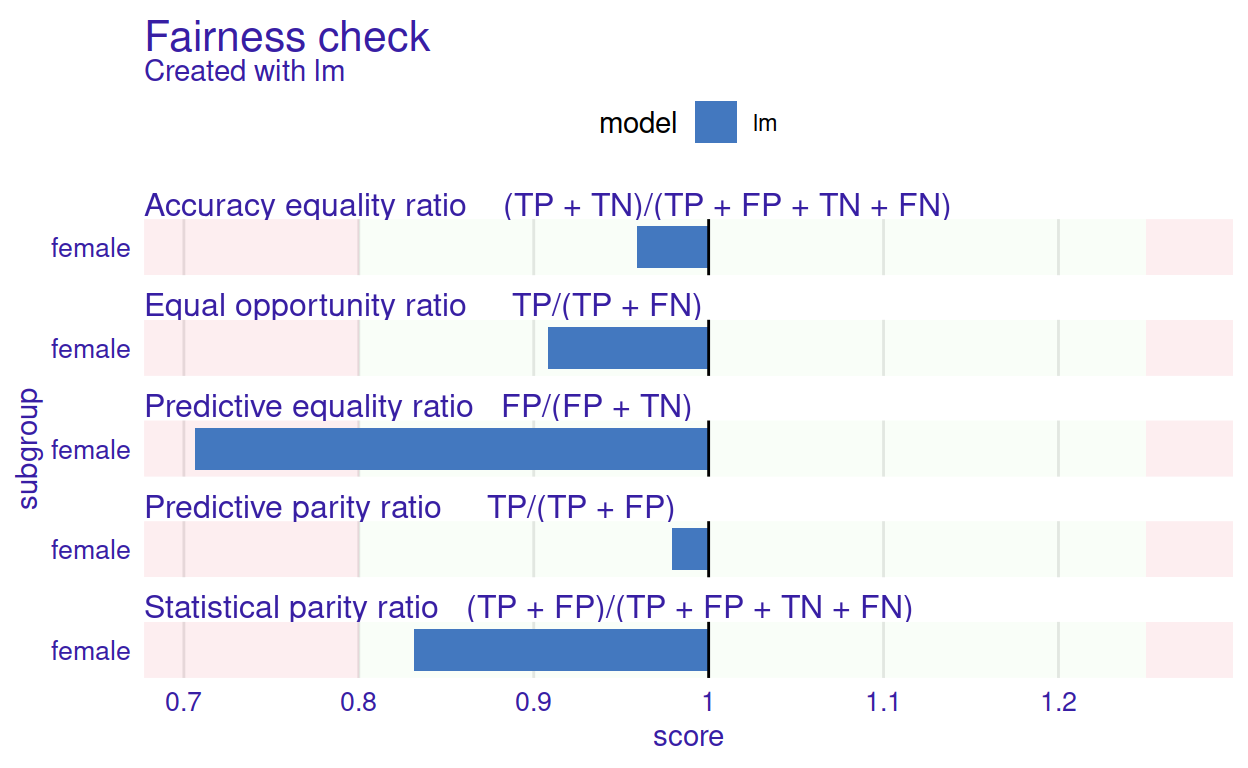
$The Fairness Check plot summarises the ratio of fairness measures between unprivileged and privileged subgroups. The light green areas correspond to values within $(\varepsilon, \frac{1}{\varepsilon})$ and signify an acceptable difference in fairness metrics. They are bounded by red rectangles indicating values that do not meet the 4/5 rule. Fairness metrics names are given along the formulas used to calculate the score in some subgroups to facilitate interpretation. For example, the ratio here means that after metric scores were calculated, the values for unprivileged groups (female) were divided by values for the privileged subgroup (male). In this example, except for the predictive equality ratio, the other measures are $\varepsilon$-non-discriminatory.$

Figure 2: The Fairness Check plot summarises the ratio of fairness measures between unprivileged and privileged subgroups. The light green areas correspond to values within $(\varepsilon, \frac{1}{\varepsilon})$ and signify an acceptable difference in fairness metrics. They are bounded by red rectangles indicating values that do not meet the 4/5 rule. Fairness metrics names are given along the formulas used to calculate the score in some subgroups to facilitate interpretation. For example, the ratio here means that after metric scores were calculated, the values for unprivileged groups (female) were divided by values for the privileged subgroup (male). In this example, except for the predictive equality ratio, the other measures are $\varepsilon$-non-discriminatory.

For a quick assessment, if a model passes fairness criteria, the object created with fairness_check() might be summarized with the print() function. Total loss is the sum of all fairness metrics. See equation (2) for more details.

print(fobject, colorize = FALSE)


Fairness check for models: lm 

lm passes 4/5 metrics
Total loss :  0.6153324

In this example, fairness criteria are satisfied in all but one metric. The logistic regression model has a lower false-positive rate (FP/(FP+TN))) in the unprivileged group than in the privileged group. It exceeds the acceptable limit set by $\varepsilon$. Thus it does not satisfy the Predictive Equality ratio criteria.

More detailed visualizations are available, like Metric scores plot. It might be helpful to understand the intuition behind the Fairness check plot presented above. See an example in Figure 3. This plot might be a good first point for understanding the Fairness check plot. In fact, checks can be directly derived from the Metric scores plot. To do this, we need to divide the score denoted by the dot with the score denoted by the vertical line. This way, we obtain a value indicated by the height of the barplot. The orientation of the barplot depends on whether the value is bigger or lower than 1. Intuitively the longer the horizontal line in the figure below (the one connecting the dot with the vertical line) is, the longer the bar will be in Fairness check plot. If the scores of privileged and unprivileged subgroups are the same, then the bar will start from 1 and point to 1, so it will have a height equal to 0.

plot(metric_scores(fobject))

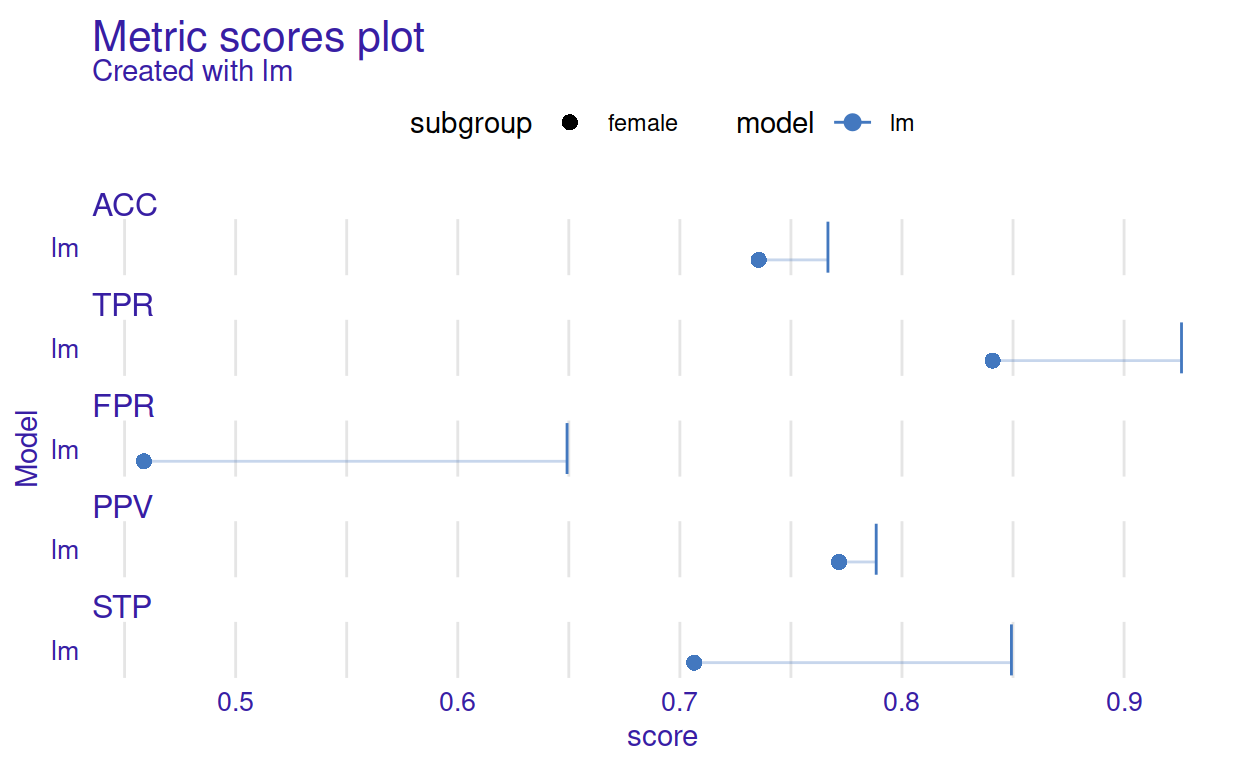
The Metric Scores plot summarises raw fairness metrics scores for subgroups. The dots stand for unprivileged subgroups (female) while vertical lines stans for the privileged subgroup (male). The horizontal lines act as a visual aid for measuring the difference between the scores of the metrics between the privileged and unprivileged subgroups.

Figure 3: The Metric Scores plot summarises raw fairness metrics scores for subgroups. The dots stand for unprivileged subgroups (female) while vertical lines stans for the privileged subgroup (male). The horizontal lines act as a visual aid for measuring the difference between the scores of the metrics between the privileged and unprivileged subgroups.

It is rare that a model perfectly meets all the fairness criteria. Therefore, a handy feature is the ability to compare several models on the same scale. We add two more explainers to the fairness assessment in the example below. Now fairness_object (in code: fobject) wraps three models together with different labels and cutoffs for subgroups. The fairness_object can be later used as a basis for another fairness_object. In detail, while running fairness_check() for the first time, explainer/explainers have to be provided along with three arguments described at the start of this section. However, as shown below, when providing explainers with a fairness_object, those arguments are not necessary as they are already a part of the previously created fairness_object.

First, let us create two more models based on the German Credit Data. The first will be a logistic regression model that uses fewer columns and has access to the Sex feature. The second is random forest from ranger (Wright and Ziegler 2017). It will be trained on the whole dataset.

discriminative_lm_model <- glm(Risk~.,
         data   = german[c("Risk", "Sex","Age",
                "Checking.account", "Credit.amount")],
         family = binomial(link = "logit"))

library("ranger")
rf_model <- ranger::ranger(Risk ~.,
         data = german, probability = TRUE,
         max.depth = 4, seed = 123)

These models differ in the way how the predict function works. To unify operations on these models, we need to create DALEX explainer objects. The label argument specifies how these models are named on plots.

explainer_dlm <- DALEX::explain(discriminative_lm_model,
        data = german[c("Sex", "Age", "Checking.account", "Credit.amount")],
        y = y_numeric,
        label = "discriminative_lm") 

explainer_rf <- DALEX::explain(rf_model, 
        data = german[,-1], y = y_numeric)

Now we are ready to assess fairness. The resulting plot is presented in Figure 4.

fobject <- fairness_check(explainer_rf, explainer_dlm, fobject)
plot(fobject)

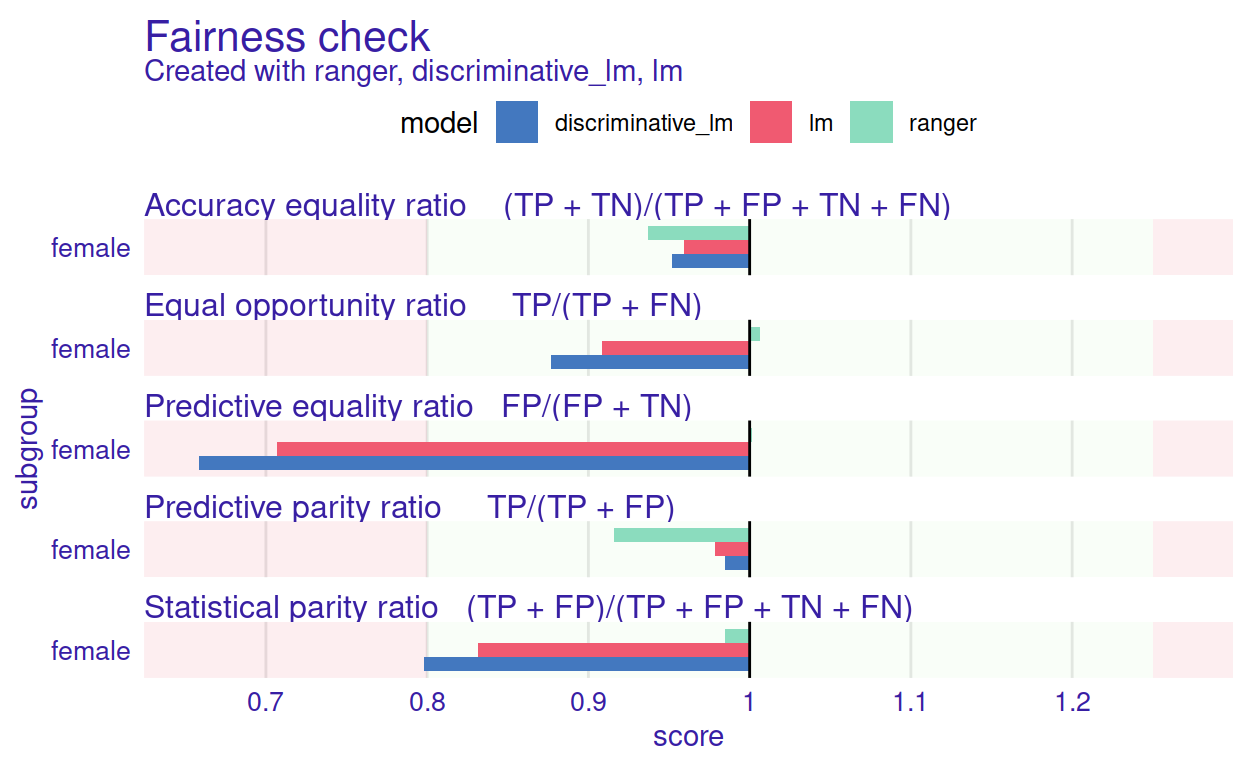
Figure 4: The Fairness Check plot for multiple models. It helps to compare models based on five selected fairness measures.

When plotted, new bars appear on the fairness check plot. Those are new metric scores for added models. This information can be summarized in a numerical way with the print() function.

print(fobject, colorize = FALSE)


Fairness check for models: ranger, discriminative_lm, lm 

ranger passes 5/5 metrics
Total loss :  0.1699186 

discriminative_lm passes 3/5 metrics
Total loss :  0.7294678 

lm passes 4/5 metrics
Total loss :  0.6153324

Package architecture

The fairmodels package provides a unified interface for predictive models independently of their internal structure. Using a model agnostic approach with DALEX explainers facilitates this process (Biecek 2018). There is a unified way for each explainer to check if explained model lives up to user fairness standards. Checking fairness with fairmodels is straightforward and can be done with the three-step pipeline.

classification model   |>   explain()   |>   fairness_check()

The output of such a pipeline is an object of class fairness_object, a unified structure to wrap model explainer or multiple model explainers and other fairness_objects in a single container. Aggregation of fairness measures is done based on groups defined by model labels. This is why model explainers (even those wrapped by fairness_objects) must have different labels. Moreover, some visualizations for model comparison assume that all models are created from the same data. Of course, each model can use different variables or different feature transformations, but the order and number of rows shall stay the same. To facilitate aggregation of models fairmodels allows creating fairness_objects in other ways:

explainers |> fairness_check() - possibly many explainers can be passed to fairness_check(),
fairness_objects |> fairness_check() - explainers stored in fairness_objects passed to fairness_check() will be aggregated into one fairness_object,
explainer & fairness_objects |> fairness_check() - explainers passed directly and explainers from fairness_objects will be aggregated into one fairness_object.

When using the last two pipelines, protected vectors and privileged parameters are assumed to be the same, so passing them to fairness_check() is unnecessary.

To create a fairness_object, at least one explainer needs to be passed to fairness_check() function, which returns the said object. fairness_object metrics for each subgroup are calculated from the separate confusion matrices.

The fairness_object has numerous fields. Some of them are:

parity_loss_metric_data - data.frame containing parity loss for each metric and classifier,
groups_data - list of metric scores for each metric and model,
group_confusion_matrices - list of values in confusion matrices for each model and metric,
explainers - list of DALEX explainers. When explainers and/or fairness_object are added, then explainers and/or explainers extracted from fairness_object are added to that list,
label - character vector of labels for each explainer.
... - other fields.

The fairness_object methods are used to create numerous objects that help to visualize bias. In the next sections, we list more detailed functions for deeper exploration of bias. Detailed relations between objects created with fairmodels are depicted in Figure 5. The general overview of the workflow is presented in Figure 6.

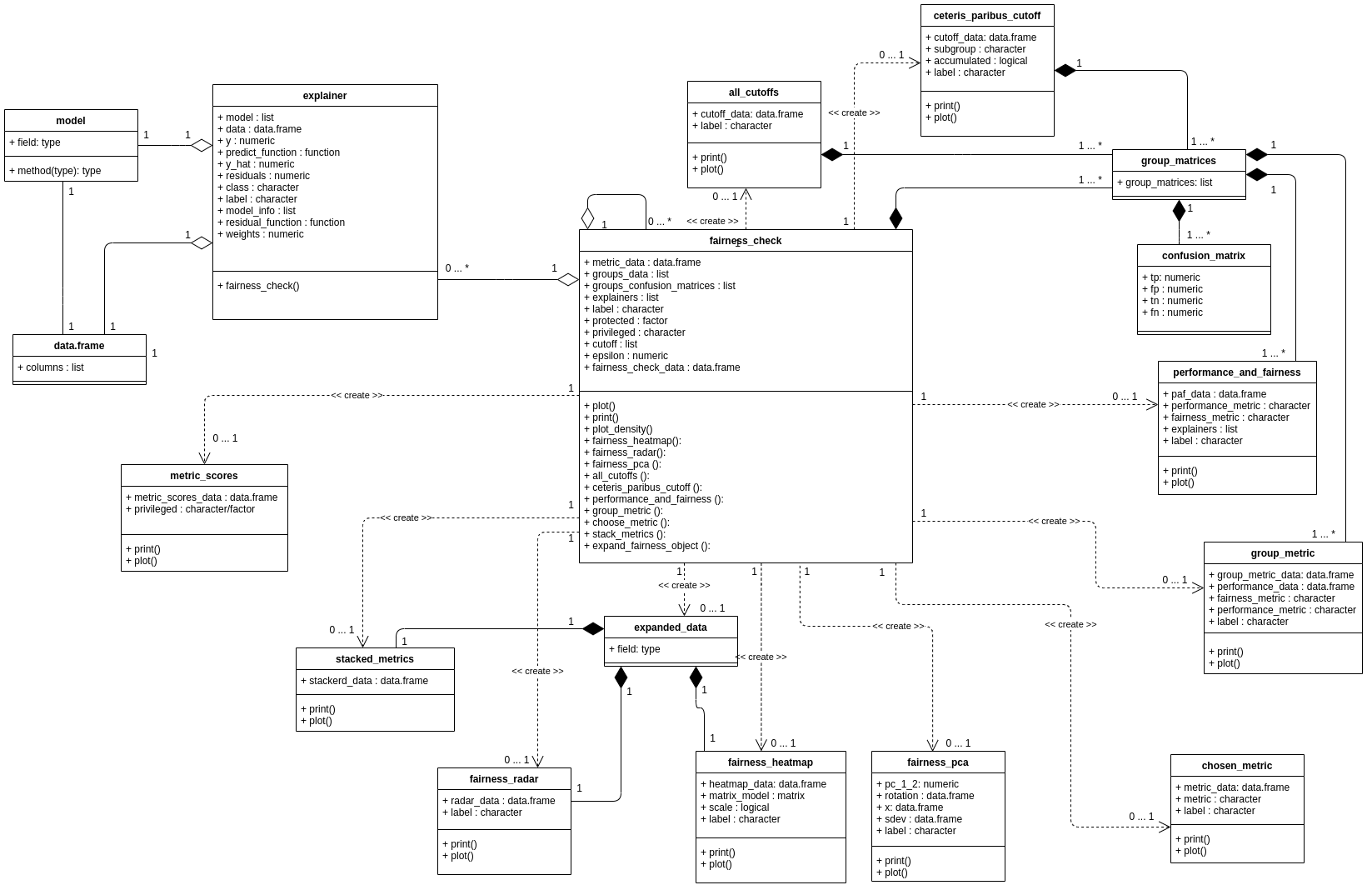
Class diagram for objects created by functions from the fairmodels package. Each rectangle corresponds to one class, the name of this class is in the header of the rectangle. Each of these classes is a list containing a certain list of objects. The top slot lists the names and types of each object the list. The bottom slot contains a list of functions that can be performed on objects of the specified class. If two classes are connected by a line ending in a diamond it means that one class contains objects of the other class. If two rectangles are connected by a dashed line, it means that on the basis of one object, an object of another class can be produced. In this case, more detailed fairness statistics can be produced from the central object of the fairness check class. See the full resolution at https://bit.ly/3HNbNvo

Figure 5: Class diagram for objects created by functions from the fairmodels package. Each rectangle corresponds to one class, the name of this class is in the header of the rectangle. Each of these classes is a list containing a certain list of objects. The top slot lists the names and types of each object the list. The bottom slot contains a list of functions that can be performed on objects of the specified class. If two classes are connected by a line ending in a diamond it means that one class contains objects of the other class. If two rectangles are connected by a dashed line, it means that on the basis of one object, an object of another class can be produced. In this case, more detailed fairness statistics can be produced from the central object of the fairness check class. See the full resolution at https://bit.ly/3HNbNvo

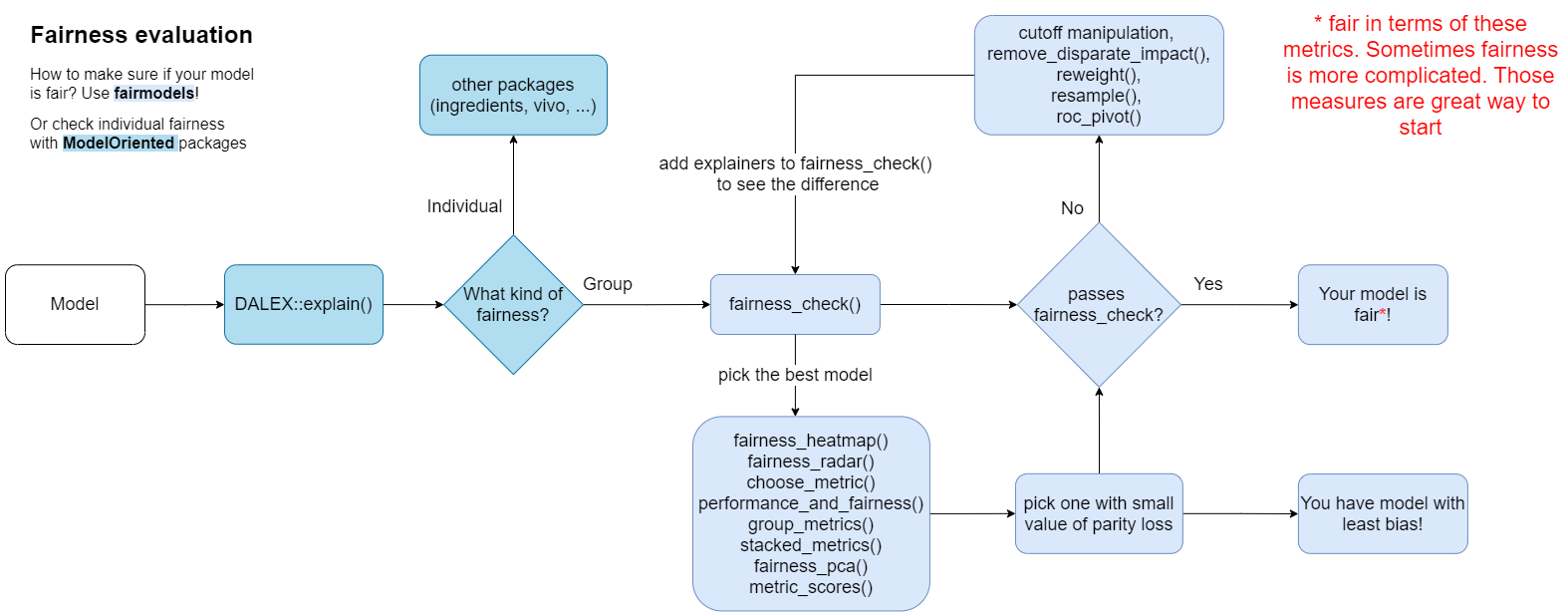
Flowchart for the fairness assessment with the fairmodels package. The arrows describe typical sequences of actions when exploring the fairness of the models. For ease of use, the names of the functions that can be used in a given step are indicated. Note that this procedure is intended to look at the model from multiple perspectives in order to track down potential problems in the model. Merely satisfying the fairness criteria does not automatically mean that the model is free of any errors

Figure 6: Flowchart for the fairness assessment with the fairmodels package. The arrows describe typical sequences of actions when exploring the fairness of the models. For ease of use, the names of the functions that can be used in a given step are indicated. Note that this procedure is intended to look at the model from multiple perspectives in order to track down potential problems in the model. Merely satisfying the fairness criteria does not automatically mean that the model is free of any errors

Visualizing bias

In fairmodels there are 12 metrics based on confusion matrices for each subgroup, see the following table for the complete list. Some of them were already introduced before.

Fairness metrics implemented in the **fairmodels** package.
Metric	Formula	Name	Fairness criteria
TPR	$\frac{TP}{TP + FN}$	True positive rate	Equal opportunity (Hardt et al. 2016)
TNR	$\frac{TN}{TN + FP}$	True negative rate
PPV	$\frac{TP}{TP + FP}$	Positive predictive value	Predictive parity (Chouldechova 2016)
NPV	$\frac{TN}{TN + FN}$	Negative predictive value
FNR	$\frac{FN}{FN + TP}$	False negative rate
FPR	$\frac{FP}{FP + TN}$	False positive rate	Predictive equality (Corbett-Davies et al. 2017)
FDR	$\frac{FP}{FP + TP}$	False discovery rate
FOR	$\frac{FN}{FN + TN}$	False omission rate
TS	$\frac{TP}{TP + FN + FP}$	Threat score
F1	$\frac{2 \cdot PPV * TPR}{PPV + TPR}$	F1 score
STP	$\frac{TP + FP}{TP + FP + TN + FN}$	Positive rate	Statistical parity
ACC	$\frac{TP + TN}{TP + TN + FP + FN}$	Accuracy	Overall accuracy equality

Not all metrics are needed to determine if the discrimination exists, but they are helpful to acquire a fuller picture. To facilitate the visualization over many subgroups, we introduce a function that maps metric scores among subgroups to a single value. This function, which we call parity_loss, has an attractive property. Due to the usage of the absolute value of the natural logarithm, it will return the same value whether the ratio is inverted or not.

So, for example, when we would like to know the parity loss of Statistical Parity between unprivileged (b) and privileged (a) subgroups, we mean value like this:

\[\begin{equation} STP_{\textit{parity loss}} = \Big | \ln \Big( \frac{STP_b}{STP_a} \Big)\Big|. \end{equation}\]

This notation is very helpful because it allows to accumulate $STP_{\textit{parity loss}}$ overall unprivileged subgroups, so not only in the binary case.

\[\begin{equation} STP_{\textit{parity loss}} = \sum_{i \in \{a, b, ...\}} \Big|\ln \Big(\frac{STP_i}{STP_a} \Big)\Big|. \tag{2} \end{equation}\]

The parity_loss relates strictly to ratios. The classifier is more fair if parity_loss is low. This property is helpful in visualizations.

There are several modifying functions that operate on fairness_object. Their usage will return other objects. The relations between them is depicted on the class diagram (Figure 5). The objects can then be plotted with a generic plot() function. Additionally, a special plotting function works immediately on fairness_object, which is plot_density. The user can directly specify which metrics shall be visible in the plot in some functions. The detailed technical introduction for all these functions is presented in fairmodels.

Plots visualizing different aspects of parity_loss can be created with one of the following pipelines:

fairness_object |> modifying_function(...) |> plot()
This pipe is preferred and allows setting parameters in both modifying functions and certain plot functions, which is not the case with the next pipeline.
fairness_object |> plot_fairmodels(type = modifying_function, ...)
Additional parameters are passed to the modifying functions and not to the plot function.

Using the pipelines, different plots can be obtained by superseding the modifying_function with function names. Four examples of additional graphical functions available in the fairmodels can be seen in Figure 7. This package implements a total of 8 different diagnostic plots, each describing a different fairness perspective. To see different aspects of fairness and bias, the user can choose the model with the smallest bias, find out the similarity between metrics and models, compare models in both fairness and performance, and see how cutoff manipulation might change the parity_loss. Find more information about each of them in the documentation.

fp1  <- plot(ceteris_paribus_cutoff(fobject, "male", cumulated=TRUE))
fp2  <- plot(fairness_heatmap(fobject))
fp3  <- plot(stack_metrics(fobject))
fp4  <- plot(plot_density(fobject))

library("patchwork")
fp1 + fp2 + fp3 + fp4 + 
  plot_layout(ncol = 2)

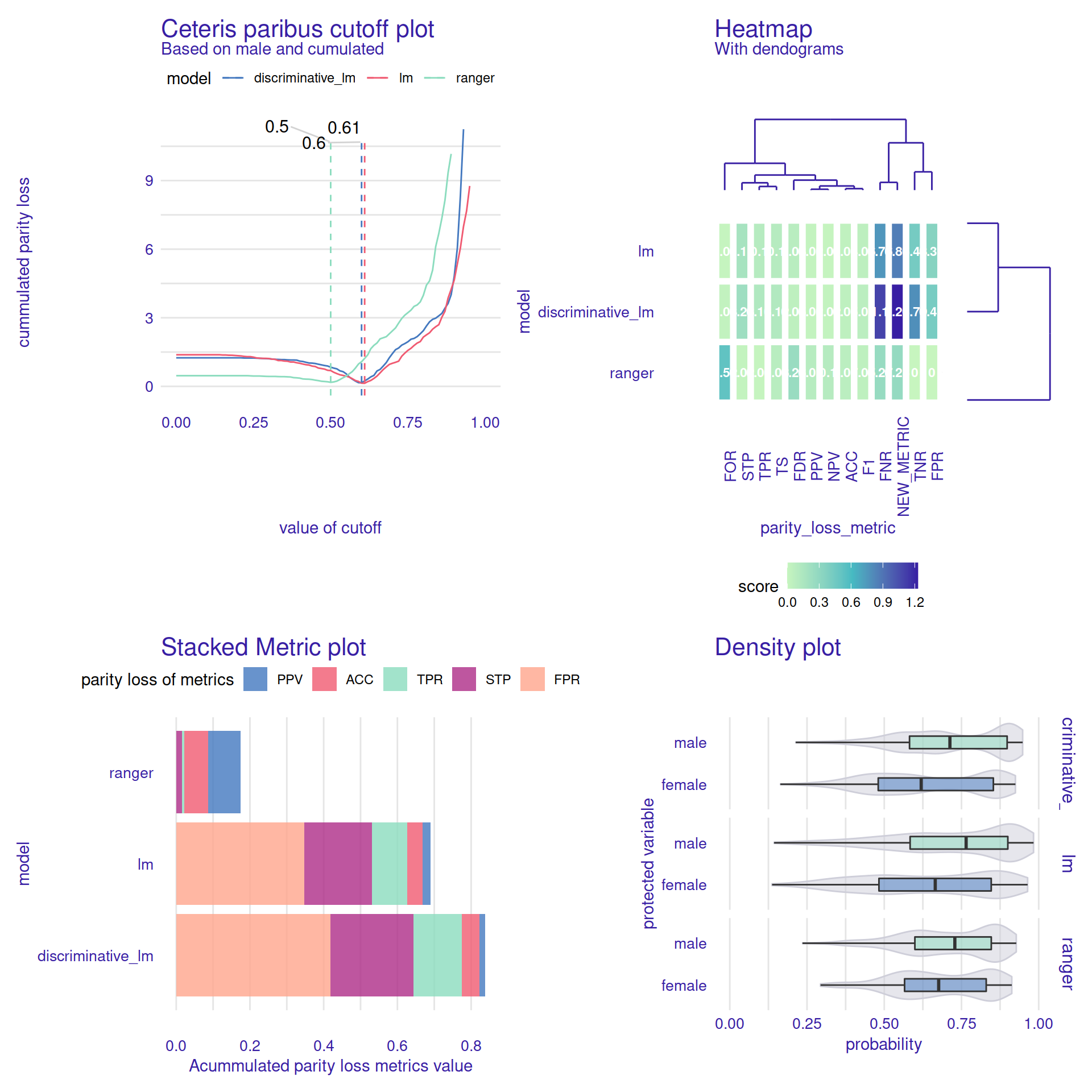
Four examples of additional graphical functions are available in the fairmodels package that facilitates model and bias exploration. The Ceteris Paribus Cuttoff plot helps select the cutoff values for each model to maximize a particular measure of fairness. In this case, the suggested cutoff point for both linear models is similar. However, the ranger model does not have calibrated probabilities and thus requires a different cutoff. The Heatmap plot is very helpful when comparing large numbers of models. It shows profiles of selected fairness measures for each of the models under consideration. In this case, the fairness profiles for both linear models are similar. The Stacked Metric plot helps you compare models by summing five different fairness measures. The different layers of this plot allow you to compare individual measures, but if you don't know which one to focus on, it is useful to look at the sum of the measures. In this case, the ranger model has the highest fairness values. Finally, the Density plot helps to compare the score distributions of the models between the advantaged and disadvantaged groups. In this case, we find that for females the distributions of the scores are lower in all models, with the largest difference for the lm model.

Figure 7: Four examples of additional graphical functions are available in the fairmodels package that facilitates model and bias exploration. The Ceteris Paribus Cuttoff plot helps select the cutoff values for each model to maximize a particular measure of fairness. In this case, the suggested cutoff point for both linear models is similar. However, the ranger model does not have calibrated probabilities and thus requires a different cutoff. The Heatmap plot is very helpful when comparing large numbers of models. It shows profiles of selected fairness measures for each of the models under consideration. In this case, the fairness profiles for both linear models are similar. The Stacked Metric plot helps you compare models by summing five different fairness measures. The different layers of this plot allow you to compare individual measures, but if you don’t know which one to focus on, it is useful to look at the sum of the measures. In this case, the ranger model has the highest fairness values. Finally, the Density plot helps to compare the score distributions of the models between the advantaged and disadvantaged groups. In this case, we find that for females the distributions of the scores are lower in all models, with the largest difference for the lm model.

Bias mitigation

What can be done if the model does not meet the fairness criteria? Machine learning practitioners might use other algorithms or variables to construct unbiased models, but this does not guarantee passing the fairness_check(). An alternative is to use bias mitigation techniques that adjust the data or model to meet fairness conditions. There are essentially three types of such methods. The first is data pre-processing. There are many ways to “correct” the data when there are unwanted correlations between variables or sample sizes among subgroups in data. The second one is in-processing, which is, for example, optimizing classifiers not only to reduce classification error but also to minimize a fairness metric. Last but not least is post-processing which modifies model output so that predictions and miss-predictions among subgroups are more alike.

The fairmodels package offers five functions for bias mitigation, three for pre-processing, and two for post-processing. Most of these approaches are also implemented in (Bellamy et al. 2018). However, in fairmodels there are separate implementations of them in R. There are a lot of useful mitigation techniques that are not in fairmodels like those in Hardt et al. (2016) and numerous in-processing algorithms.

Data pre-processing

Disparate impact remover
In fairmodels geometric repair, an algorithm originally introduced by Feldman et al. (2015), works on ordinal, numeric features. Depending on the $\lambda \in [0,1]$ parameter, this method will transform the distribution of a given feature. The idea is simple. Given feature distribution in different subgroups, the algorithm finds optimal distribution (according to earth mover’s distance) and transforms distribution for each subgroup to match the optimal one. For example, if age is an important feature and its distribution is different in two subgroups, and we want to change that, then the geometric repair will map each individual’s age to a new distribution (different age). It will be preserving the order - the ranks (in our case, seniority) of observations are preserved. Parameter $\lambda$ is responsible for the repair degree, so for full repair, lambda should be set to 1. The method does not focus on a particular metric but rather tries to level out them by transforming potentially harmful feature distributions.
Reweighting
Reweighting is a rather straightforward approach. This method was implemented according to Kamiran and Calders (2011). It computes weights by dividing the theoretical probability of assigning favorable labels for a subgroup by real (observed) probability (based on the data). Theoretic probability for a subgroup is computed by multiplying the probability of assigning a favorable label (for all populations) by picking observation from a certain subgroup. It focuses on mitigating statistical parity.
Resampling
Resampling is based on weights calculated in reweighting. Each weight for a subgroup is multiplied by the size of the subgroup. Then, whether the subgroup is deprived or not (if weight is higher than one, the subgroup is considered deprived), observations are duplicated from either one that were assigned a favorable label or not. There are two types of resampling- uniform and preferential. The uniform is making algorithm pick or omit observations randomly without considering its probabilistic score. Preferential uses another probabilistic classifier, potentially different from the main model for final predictions. In Kamiran and Calders (2011) it is called ranker - it predicts the probabilities for the observations to decide which observations are close to the cutoff border (usually 0.5). Based on the probabilistic output of the ranker, the observations are sorted, and the ones with the highest/lowest ranks are either left out or duplicated depending on the case—more on that on Kamiran and Calders (2011). The fairmodels implementation, instead of training the ranker as in the aforementioned paper, uses a vector of previously calculated probabilities provided by the user. With this, it shifts the decision and responsibility of choosing a ranker to the user. It focuses on mitigating statistical parity.

Model post-processing

Reject Option based Classification Pivot
The roc_pivot method is implemented based on Kamiran et al. (2012) in the fairmodels package. Let $\theta \in (0,1)$ be the value that determines the radius of the so-called critical region, which is an area around the cutoff. The user specifies the $\theta$, and it should describe how big the critical region should be. For example if $\theta = 0.1$ and cutoff is 0.6, then the critical region will be (0.5, 0.7). Let’s assume that we are predicting a favorable outcome. If the assigned probability of observation is in the described region, then the probabilities are pivoting on the other side of the cutoff with a certain assumption. If an observation in a critical region is considered to be the privileged and it is on the right side of the cutoff, then its probabilities are pivoting from the right side of the cutoff to the left. So if an observation is in the critical region and it is considered unprivileged, then if it is on the left side of the cutoff, it will pivot to the right side. Pivoting here means changing the side of the cutoff so that the distance from the cutoff stays unchanged. It does not intend to mitigate a single metric but rather changes predictions in the critical region (the region with low certainty). By pivoting the predictions, it might lower more metrics.
Cutoff manipulation
The fairmodels package supports setting cutoff for each subgroup. Users may pick parity_loss metrics of their choice and find the minimal parity_loss. It is part of ceteris_paribus_cutoff() function. Based on picked metrics, the sum of parity loss is calculated for each cutoff of the chosen subgroup. Then the minimal value is found—this way, optimal values might be found for metrics of interest. The minimum is marked with a dashed vertical line (see Figure 7). This approach however might be to some extent concerning. Some might argue that setting different cutoffs for different subgroups is unfair and is punishing privileged subgroups for something they have no control of. Especially in the individual fairness field, it would be concerning if two similar people with different sensitive attributes would have two different thresholds and potentially two different outcomes. This is a valid point, and this method should be used with knowledge of all its drawbacks. The cutoff manipulation method targets metrics chosen by the user.

All pre-processing methods can be used with two pipelines, whereas post-processing can be used in one specific way.

Pre-processing pipelines
- data/explainer |> method
  Returns either weights, indexes, or changed data depending on the method used.
- data/explainer |> pre_process_data(data, protected, y, type = ...)
  Always returns data.frame. In case of weights data has additional column called _weights_.
Post-processing pipelines
- fairness_object |> ceteris_paribus_cutoff(subgroup, ...) |> print/plot
  This is the pipeline for creating ceteris paribus cutoff print and plot.
- explainer |> roc_pivot(protected, privileged, ...)
  The pipeline will return explainer with y_hat field changed.

The user should be aware that debiasing one metric might enhance bias in another. It is a so-called fairness-fairness trade-off. There is also a fairness-performance trade-off where debiasing one metric leads to worse performance. Another thing to remember is, as found in Agrawal et al. (2020), metrics might not generalize well to out-of-distribution examples, so it is advised also to check the fairness metrics on a separate test set.

Example

Now we will show an example usage of one pre-processing and one post-processing method. As before, the German Credit Data will be used along with the previously created lm_model. So firstly, we create a new dataset using pre_process_data and then we use it to train the logistic regression classifier.

resampled_german   <- german |> pre_process_data(protected = german$Sex,
                y_numeric, type = 'resample_uniform')

lm_model_resample  <- glm(Risk~.,
                data   = resampled_german,
                family = binomial(link = "logit"))

explainer_lm_resample <- DALEX::explain(lm_model_resample,
                data = german[,-1], y = y_numeric, verbose = FALSE)

Then we make other explainers. We use previously created explainer_lm with the post-processing function roc_pivot. We set parameter theta = 0.05 for a rather narrow area of a pivot.

new_explainer <- explainer_lm |> roc_pivot(protected = german$Sex,
                privileged = "male", theta = 0.05)

In the end, we create fairness_object with explainers obtained with the code above and one created in the first example to see the difference.

fobject <- fairness_check(explainer_lm_resample, new_explainer, explainer_lm,
                protected = german$Sex, privileged = "male",
                label = c("resample", "roc", "base"),
                verbose = FALSE)

fobject |> plot()

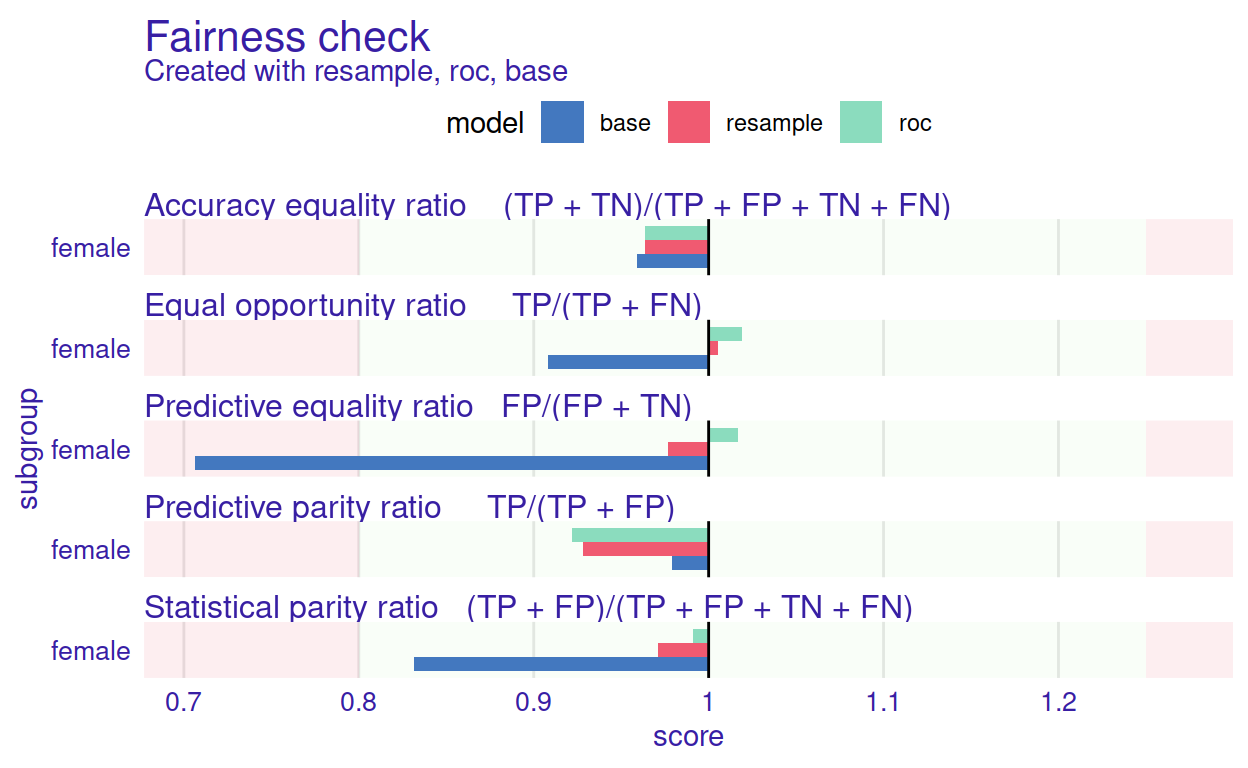
Graphical summary of a base model (blue bars) and model after applying two bias mitigation techniques (red and green bars). By comparing adjacent rectangles one can read how the respective technique affected the corresponding fairness measure

Figure 8: Graphical summary of a base model (blue bars) and model after applying two bias mitigation techniques (red and green bars). By comparing adjacent rectangles one can read how the respective technique affected the corresponding fairness measure

The result of the code above is presented in Figure 8. The mitigation methods successfully eliminated bias in all of the metrics. Both models are better than the original base. This is not always the case - sometimes, eliminating bias in one metric may increase bias in another metric. For example, let’s consider a perfectly accurate model, but some subgroups receive few positive predictions (bias in Statistical parity). In that case, mitigating the bias in Statistical parity would decrease the Accuracy equality ratio.

Summary and future work

This paper showed that checking for bias in machine learning models can be done conveniently and flexibly. The package fairmodels described above is a self-sufficient tool for bias detection, visualization, and mitigation in classification machine learning models. We presented theory, package architecture, suggested usage, and examples along with plots. Along the way, we introduced the core concepts and assumptions that come along the bias detection and plot interpretation. The package is still improved and enhanced, which can be seen by adding the announced regression module based on Steinberg et al. (2020). We did not cover it in this article because it is still an experimental tool. Another tool for in-processing classification closely related to fairmodels has also been added and can be found on https://github.com/ModelOriented/FairPAN.

The source code of the package, vignettes, examples, and documentation can be found at https://modeloriented.github.io/fairmodels/. The stable version is available on CRAN. The code and the development version can be found on GitHub https://github.com/ModelOriented/fairmodels. This is also a place to report bugs or requests (through GitHub issues).

In the future, we plan to enhance the spectrum of bias visualization plots and introduce regression and individual fairness methods. The potential way to explore would be an in-processing bias mitigation - training models that minimize cost function and adhere to certain fairness criteria. This field is heavily developed in Python and lacks appropriate attention in R.

Acknowledgements

Work on this package was financially supported by the NCN Sonata Bis-9 grant 2019/34/E/ST6/00052.

Supplementary materials

Supplementary materials are available in addition to this article. It can be downloaded at RJ-2022-019.zip

CRAN packages used

fairmodels, h2o, fairness, fairadapt, DALEX, ranger

CRAN Task Views implied by cited packages

HighPerformanceComputing, MachineLearning, ModelDeployment, Survival, TeachingStatistics

A. Agrawal, F. Pfisterer, B. Bischl, J. Chen, S. Sood, S. Shah, F. Buet-Golfouse, B. A. Mateen and S. Vollmer. Debiasing classifiers: Is reality at variance with expectation? Electronic, 2020.

J. Angwin, J. Larson, S. Mattu and and Lauren Kirchner. Machine bias: There’s software used across the country to predict future criminals. And it’s biased against blacks. ProPublica, 2016. URL https://www.propublica.org/article/machine-bias-risk-assessments-in-criminal-sentencing.

S. Barocas, M. Hardt and A. Narayanan. Fairness and machine learning. fairmlbook.org, 2019. http://www.fairmlbook.org.

R. K. E. Bellamy, K. Dey, M. Hind, S. C. Hoffman, S. Houde, K. Kannan, P. Lohia, J. Martino, S. Mehta, A. Mojsilovic, et al. AI Fairness 360: An extensible toolkit for detecting, understanding, and mitigating unwanted algorithmic bias. 2018. URL https://arxiv.org/abs/1810.01943.

R. Berk, H. Heidari, S. Jabbari, M. Kearns and A. Roth. Fairness in criminal justice risk assessments: The state of the art. Sociological Methods & Research, 2017. URL https://doi.org/10.1177/0049124118782533.

P. Biecek. DALEX: Explainers for Complex Predictive Models in R. Journal of Machine Learning Research, 19(84): 1–5, 2018. URL http://jmlr.org/papers/v19/18-416.html.

P. Biecek and T. Burzykowski. Explanatory Model Analysis. Chapman; Hall/CRC, New York, 2021. URL https://pbiecek.github.io/ema/.

R. Binns. On the apparent conflict between individual and group fairness. In Proceedings of the 2020 conference on fairness, accountability, and transparency, pages. 514–524 2020. New York, NY, USA: Association for Computing Machinery. ISBN 9781450369367. URL https://doi.org/10.1145/3351095.3372864.

S. Bird, M. Dudík, R. Edgar, B. Horn, R. Lutz, V. Milan, M. Sameki, H. Wallach and K. Walker. Fairlearn: A toolkit for assessing and improving fairness in AI. MSR-TR-2020-32. Microsoft. 2020. URL https://www.microsoft.com/en-us/research/publication/fairlearn-a-toolkit-for-assessing-and-improving-fairness-in-ai/.

J. Buolamwini and T. Gebru. Gender shades: Intersectional accuracy disparities in commercial gender classification. In Proceedings of the 1st conference on fairness, accountability and transparency, Eds S. A. Friedler and C. Wilson pages. 77–91 2018. New York, NY, USA. URL http://proceedings.mlr.press/v81/buolamwini18a.html.

A. Chouldechova. Fair prediction with disparate impact: A study of bias in recidivism prediction instruments. Big Data, 5: 2016. URL https://doi.org/10.1089/big.2016.0047.

D. Cirillo, S. Catuara-Solarz, C. Morey, E. Guney, L. Subirats, S. Mellino, A. Gigante, A. Valencia, M. J. Rementeria, A. S. Chadha, et al. Sex and gender differences and biases in artificial intelligence for biomedicine and healthcare. npj Digital Medicine, 3(1): 81, 2020. URL https://doi.org/10.1038/s41746-020-0288-5 [online; last accessed October 24, 2021].

Code of Federal Regulations. SECTION 4D, UNIFORM GUIDELINES ON EMPLOYEE SELECTION PROCEDURES (1978). 1978. URL https://www.govinfo.gov/content/pkg/CFR-2014-title29-vol4/xml/CFR-2014-title29-vol4-part1607.xml.

S. Corbett-Davies, E. Pierson, A. Feller, S. Goel and A. Huq. Algorithmic decision making and the cost of fairness. In Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining, pages. 797–806 2017. New York, NY, USA: Association for Computing Machinery. URL https://doi.org/10.1145/3097983.3098095.

Council of Europe. Guidelines on facial recognition. 2021. URL https://www.coe.int/en/web/portal/-/facial-recognition-strict-regulation-is-needed-to-prevent-human-rights-violations-.

D. Dua and C. Graff. UCI machine learning repository. 2017. URL https://archive.ics.uci.edu/ml/datasets/statlog+(german+credit+data).

C. Dwork, M. Hardt, T. Pitassi, O. Reingold and R. Zemel. Fairness through awareness. In Proceedings of the 3rd innovations in theoretical computer science conference, pages. 214–226 2012. New York, NY, USA: Association for Computing Machinery. URL https://doi.org/10.1145/2090236.2090255.

European Union Agency for Fundamental Rights and Council of Europe. Handbook on european non-discrimination law. Luxembourg: Publications Office of the European Union, 2018. https://fra.europa.eu/en/publication/2018/handbook-european-non-discrimination-law-2018-edition.

European Union Agency for Fundamental Rights. Handbook on european non-discrimination law. 2018. DOI https://doi.org/10.2811/792676.

M. Feldman, S. A. Friedler, J. Moeller, C. Scheidegger and S. Venkatasubramanian. Certifying and removing disparate impact. In Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining, pages. 259–268 2015. New York, NY, USA: Association for Computing Machinery. URL https://doi.org/10.1145/2783258.2783311.

H2O.ai. H2O AutoML. 2017. URL http://docs.h2o.ai/h2o/latest-stable/h2o-docs/automl.html. H2O version 3.30.0.1.

M. Hardt, E. Price, E. Price and N. Srebro. Equality of opportunity in supervised learning. In Advances in neural information processing systems 29, Eds D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon and R. Garnett pages. 3315–3323 2016. Curran Associates, Inc. URL http://papers.nips.cc/paper/6374-equality-of-opportunity-in-supervised-learning.pdf.

F. Kamiran and T. Calders. Data pre-processing techniques for classification without discrimination. Knowledge and Information Systems, 33: 2011. URL https://doi.org/10.1007/s10115-011-0463-8.

F. Kamiran, A. Karim and X. Zhang. Decision theory for discrimination-aware classification. In 2012 IEEE 12th international conference on data mining, pages. 924–929 2012. URL https://doi.org/10.1109/ICDM.2012.45.

N. Kozodoi, J. Jacob and S. Lessmann. Fairness in credit scoring: Assessment, implementation and profit implications. European Journal of Operational Research, 2021. URL https://doi.org/10.1016/j.ejor.2021.06.023.

N. Kozodoi and T. V. Varga. Fairness: Algorithmic fairness metrics. 2021. URL https://CRAN.R-project.org/package=fairness. R package version 1.2.1.

P. Lahoti, K. P. Gummadi and G. Weikum. [iFair: Learning individually fair data representations for algorithmic decision making]. In 2019 IEEE 35th international conference on data engineering (ICDE), pages. 1334–1345 2019. URL https://doi.org/10.1109/ICDE.2019.00121.

N. Mehrabi, F. Morstatter, N. Saxena, K. Lerman and A. Galstyan. A survey on bias and fairness in machine learning. 2019. URL https://arxiv.org/abs/1908.09635.

D. Plečko and N. Meinshausen. Fair data adaptation with quantile preservation. 2019. URL https://arxiv.org/abs/1911.06685.

P. Saleiro, B. Kuester, A. Stevens, A. Anisfeld, L. Hinkson, J. London and R. Ghani. Aequitas: A bias and fairness audit toolkit. 2018. URL https://arxiv.org/abs/1811.05577.

D. C. Steinberg, A. Reid and S. T. O’Callaghan. Fairness measures for regression via probabilistic classification. ArXiv, abs/2001.06089: 2020.

M. Wick, S. Panda and J.-B. Tristan. Unlocking fairness: A trade-off revisited. In Advances in neural information processing systems, Eds H. Wallach, H. Larochelle, A. Beygelzimer, F. dAlché-Buc, E. Fox and R. Garnett pages. 8783–8792 2019. Curran Associates, Inc. URL https://proceedings.neurips.cc/paper/2019/file/373e4c5d8edfa8b74fd4b6791d0cf6dc-Paper.pdf.

M. N. Wright and A. Ziegler. ranger: A fast implementation of random forests for high dimensional data in C++ and R. Journal of Statistical Software, 77(1): 1–17, 2017. DOI 10.18637/jss.v077.i01.

fairmodels: a Flexible Tool for Bias Detection, Visualization, and Mitigation in Binary Classification Models

Introduction

Measuring and detecting bias

Fairness metrics

Acceptable amount of bias

Evaluating fairness

Example

Package architecture

Visualizing bias

Bias mitigation

Data pre-processing

Model post-processing

Example

Summary and future work

Acknowledgements

Supplementary materials

CRAN packages used

CRAN Task Views implied by cited packages

References

Reuse

Citation

Metric	Formula	Name	Fairness criteria
TPR	\(\frac{TP}{TP + FN}\)	True positive rate	Equal opportunity (Hardt et al. 2016)
TNR	\(\frac{TN}{TN + FP}\)	True negative rate
PPV	\(\frac{TP}{TP + FP}\)	Positive predictive value	Predictive parity (Chouldechova 2016)
NPV	\(\frac{TN}{TN + FN}\)	Negative predictive value
FNR	\(\frac{FN}{FN + TP}\)	False negative rate
FPR	\(\frac{FP}{FP + TN}\)	False positive rate	Predictive equality (Corbett-Davies et al. 2017)
FDR	\(\frac{FP}{FP + TP}\)	False discovery rate
FOR	\(\frac{FN}{FN + TN}\)	False omission rate
TS	\(\frac{TP}{TP + FN + FP}\)	Threat score
F1	\(\frac{2 \cdot PPV * TPR}{PPV + TPR}\)	F1 score
STP	\(\frac{TP + FP}{TP + FP + TN + FN}\)	Positive rate	Statistical parity
ACC	\(\frac{TP + TN}{TP + TN + FP + FN}\)	Accuracy	Overall accuracy equality

fairmodels: a Flexible Tool for Bias Detection, Visualization, and Mitigation in Binary Classification Models

Introduction

Related work

Measuring and detecting bias

Fairness metrics

Acceptable amount of bias

Evaluating fairness

Example

Package architecture

Visualizing bias

Bias mitigation

Data pre-processing

Model post-processing

Example

Summary and future work

Acknowledgements

Supplementary materials

CRAN packages used

CRAN Task Views implied by cited packages

References

Reuse

Citation