1 Introduction
This paper is about exploring longitudinal data effectively. By “longitudinal data” we specifically mean individuals repeatedly measured through time. This could include panel data, where possibly different samples from a key variable (e.g. country), are aggregated at each time collection. The important component is a key variable with repeated measurements regularly, or irregularly over time. The inherent structure allows us to examine temporal patterns of individuals, shown in Figure 1, of the average height of Australian males over years. The individual component is country, and the time component is year. The variable country along with other variables is measured repeatedly from 1900 to 1970, with irregular intervals between years.
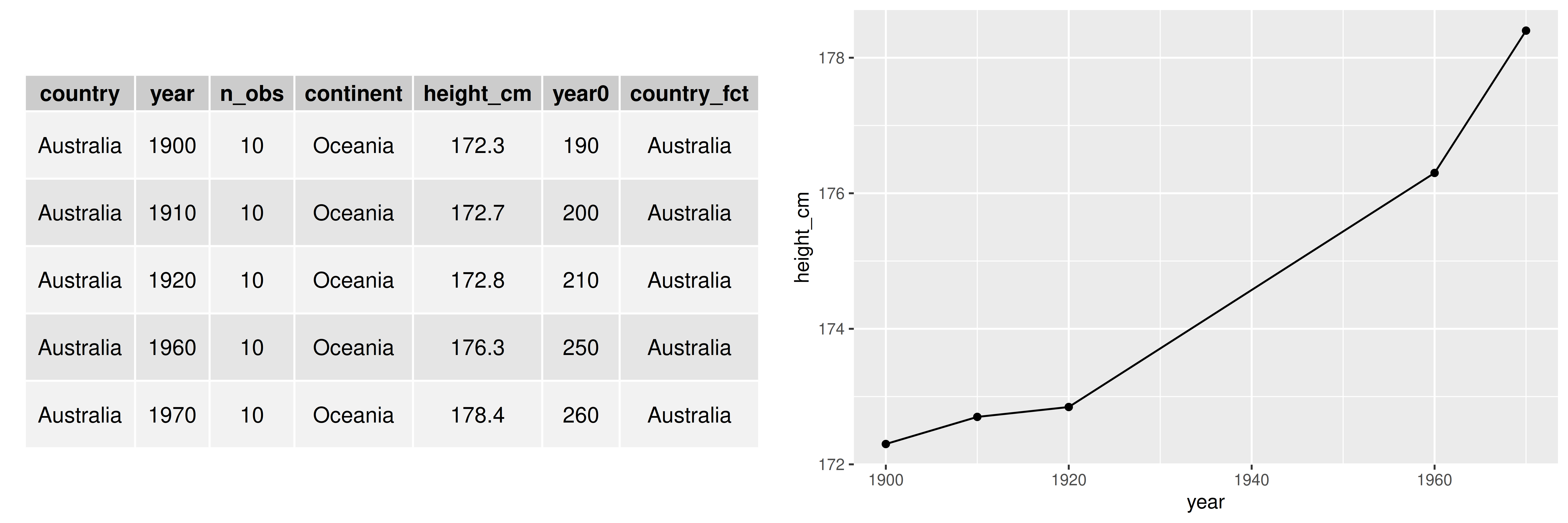
Figure 1: Example of longitudinal data: average height of men in Australia for 1900-1970. The height increase over time, and are measured at irregular intervals.
The full dataset of Figure 1 is shown in Figure 2, showing 144 countries from the year 1700. This plot is challenging to understand because there is overplotting, making it hard to see the individuals. Solutions to this are not always obvious. Showing separate individual plots of each country does not help, as 144 plots is too many to comprehend. Making the lines transparent or fitting a simple model to all the data Figure 2B, might be a common first step to see common trends. However, all this seems to clarify is: 1) There is a set of some countries that are similar, and they are distributed around the center of the countries, and 2) there is a general upward trend in heights over time. We learn about the collective, but lose sight of the individuals.
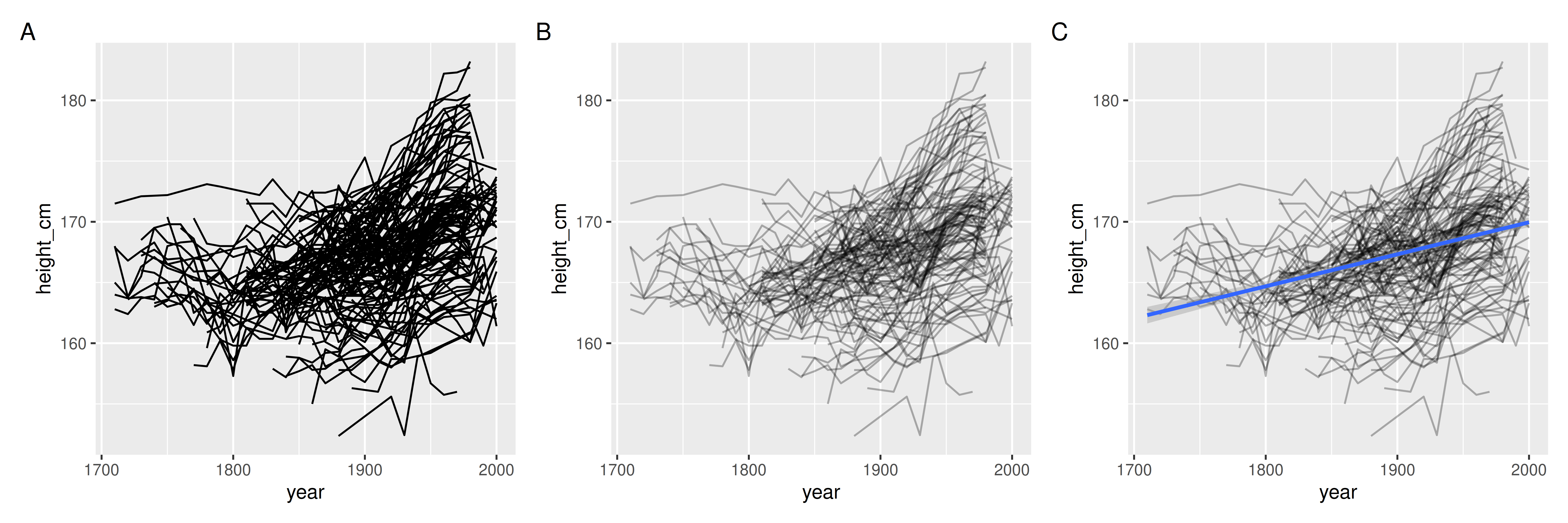
Figure 2: The full dataset shown as a spaghetti plot (A), with transparency (B), and with a linear model overlayed (C). It is still hard to see the individuals.
This paper demonstrates how to effectively and efficiently explore longitudinal data, using the R package, brolgar. We examine four problems in exploring longitudinal data:
- How to sample the data
- Finding interesting individuals
- Finding representative individuals
- Understanding a model
This paper proceeds in the following way: first, a brief review of existing approaches to longitudinal data, then the definition of longitudinal data, then approaches to these four problems are discussed, followed by a summary.
2 Background
R provides basic time series, ts, objects, which are vectors or matrices that represent data sampled at equally spaced points in time. These have been extended through packages such as xts, and zoo (Zeileis and Grothendieck 2005; Ryan and Ulrich 2020), which only consider data in a wide format with a regular implied time series. These are not appropriate for longitudinal data, which can have indexes that are not time unit oriented, such as “Wave 1…n”, or may contain irregular intervals.
Other packages focus more directly on panel data in R, focussing on data operations and model interfaces. The pmdplyr package provides “Panel Manoeuvres” in dplyr(Huntington-Klein and Khor 2020). It defines the data structure in as a pibble object (panel tibble), requiring an id and group column being defined to identify the unique identifier and grouping. The pmdplyr package focuses on efficient and custom joins and functions, such as inexact_left_join(). It does not implement tidyverse equivalent tools, but instead extends their usecase with a new function, for example mutate_cascade and mutate_subset. The panelr package provides an interface for data reshaping on panel data, providing widening and lengthening functions (widen_panel() and long_panel() (Long 2020)). It also provides model facilitating functions by providing its own interface for mixed effects models. The plm package (Millo 2017) for panel data econometrics provides methods for estimating models such as GMM for panel data, and testing, for example for model specification or serial correlation. It also provides a data structure, the pdata.frame, which stores the index attribute of the individual and time dimensions, for use within the package’s functions.
These software generally re-implement their own custom panel data class object, as well as custom data cleaning tasks, such as reshaping into long and wide form. They all share similar features, providing some identifying or index variable, and some grouping or key.
3 Longitudinal Data Structures
Longitudinal data is a sibling of many other temporal data forms, including panel data, repeated measures, and time series. The differences are many, and can be in data collection, context and even the field of research. Time series are usually long and regularly spaced in time. Panel data may measure different units at each time point and aggregate these values by a categorical or key variable. Repeated measures typically measure before and after treatment effects. We like to think of longitudinal as measuring the same individual (e.g. wage earner) over time, but this definition is not universally agreed on. Despite the differences, they all share a fundamental similarity: they are measurements over a time period.
This time period has structure - the time component (dates, times, waves, seconds, etc), and the spacing between measurements - unequal or equal. This data structure needs to be respected during analysis to preserve the lowest level of granularity, to avoid for example, collapsing across month when the data is collected every second, or assuming measurements occur at fixed time intervals. These mistakes can be avoided by encoding the data structure into the data itself. This information can then be accessed by analysis tools, providing a consistent way to understand and summarise the data. This ensures the different types of longitudinal data previously mentioned can be handled in the same way.
Building on a tsibble
Since longitudinal data can be thought of as “individuals repeatedly measured through time”, they can be considered as a type of time series, as defined in Hyndman and Athanasopoulos (2018): “Anything that is observed sequentially over time is a time series”. This definition has been realised as a time series tsibble in (Wang et al. 2020). These objects are defined as data meeting these conditions:
- The
index: the time variable - The
key: variable(s) defining individual groups (or series) - The
indexandkey(1 + 2) together determine a distinct row
If the specified key and index pair do not define a distinct row - for example, if there are duplicates in the data, the tsibble will not be created. This helps ensure the data is properly understood and cleaned before analysis is conducted, removing avoidable errors that might have impacted downstream decisions.
We can formally define our heights data from Figure 1 as a tsibble using, as_tsibble:
heights_brolgar <- as_tsibble(heights_brolgar,
index = year,
key = country,
regular = FALSE)The index is year, the key is country, and regular = FALSE since the intervals in the years measured are not regular. Using a tsibble means that the index and key time series information is recorded only once, and can be referred to many times in other parts of the data analysis by time-aware tools.
In addition to providing consistent ways to manipulate time series data, further benefits to building on tsibble are how it works within the tidyverse ecosystem, as well as the tidy time series packages called “tidyverts”, containing fable (O’Hara-Wild et al. 2020a), feasts, (O’Hara-Wild et al. 2020b). For example, tsibble provides modified tidyverse functions to explore implicit missing values in the index (e.g., has_gaps() and fill_gaps()), as well as grouping and partitioning based on the index with index_by(). For full details and examples of use with the tidyverts time series packages, see Wang et al. (2020).
The brolgar package uses tsibble so users can take advantage of these tools, learning one way of operating a data analysis that will work and have overlap with other contexts.
Characterising Individual Series
Calculating a feature
We can summarise the individual series by collapsing their many measurements into a single statistic, such as the minimum, maximum, or median, with one row per key. We do this with the features function from the fabletools package, made available in brolgar. This provides a summary of a given variable, accounting for the time series structure, and returning one row per key specified. It can be thought of as a time-series aware variant of the summarise function from dplyr. The feature function works by specifying the data, the variable to summarise, and the feature to calculate. A template is shown below
features(<DATA>, <VARIABLE>, <FEATURE>)or, with the pipe:
<DATA> %>% features(<VARIABLE>, <FEATURE>)For example, to calculate the minimum height for each key (country), in heights, we specify the heights data, then the variable to calculate features on, height_cm, then the feature to calculate, min (we write c(min = min) so the column calculated gets the name “min”):
heights_min <- features(.tbl = heights_brolgar,
.var = height_cm,
features = c(min = min))
heights_min# A tibble: 119 × 2
country min
<chr> <dbl>
1 Afghanistan 161.
2 Algeria 166.
3 Angola 159.
4 Argentina 167.
5 Armenia 164.
6 Australia 170
7 Austria 162.
8 Azerbaijan 170.
9 Bangladesh 160.
10 Belgium 163.
# … with 109 more rowsWe call these summaries features of the data. We can use this information to summarise these features of the data, for example, visualising the distribution of minimum values (Figure 3A).
We are not limited to one feature at a time, many features can also be calculated, for example:
heights_three <- heights_brolgar %>%
features(height_cm, c(
min = min,
median = median,
max = max
))
heights_three# A tibble: 119 × 4
country min median max
<chr> <dbl> <dbl> <dbl>
1 Afghanistan 161. 167. 168.
2 Algeria 166. 169 171.
3 Angola 159. 167. 169.
4 Argentina 167. 168. 174.
5 Armenia 164. 169. 172.
6 Australia 170 172. 178.
7 Austria 162. 167. 179.
8 Azerbaijan 170. 172. 172.
9 Bangladesh 160. 162. 164.
10 Belgium 163. 166. 177.
# … with 109 more rowsThese can then be visualised together (Figure 3).
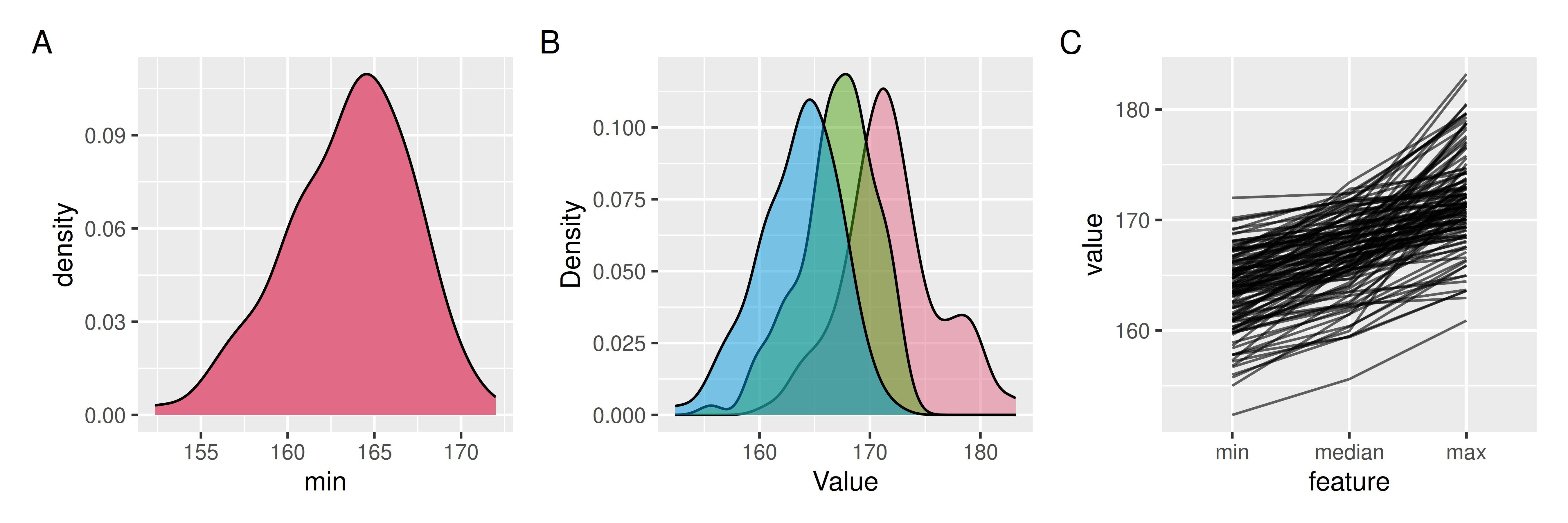
Figure 3: Three plots showing the distribution of minimum, median, and maximum values of height in centimeters. Part A shows just the distribution of minimum, part B shows the distribution of minimum, median, and maximum, and part C shows these three values plotted together as a line graph. We see that there is overlap amongst all three statistics. That is, some countries minimum heights are taller than some countries maximum heights.
These sets of features can be pre-specified, for example, brolgar provides a five number summary (minimum, 25th quantile, median, mean, 75th quantile, and maximum) of the data with feat_five_num:
heights_five <- heights_brolgar %>%
features(height_cm, feat_five_num)
heights_five# A tibble: 119 × 6
country min q25 med q75 max
<chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Afghanistan 161. 164. 167. 168. 168.
2 Algeria 166. 168. 169 170. 171.
3 Angola 159. 160. 167. 168. 169.
4 Argentina 167. 168. 168. 170. 174.
5 Armenia 164. 166. 169. 172. 172.
6 Australia 170 171. 172. 173. 178.
7 Austria 162. 164. 167. 169. 179.
8 Azerbaijan 170. 171. 172. 172. 172.
9 Bangladesh 160. 162. 162. 163. 164.
10 Belgium 163. 164. 166. 168. 177.
# … with 109 more rowsThis takes the heights data, pipes it to features, and then instructs it to summarise the height_cm variable, using feat_five_num. There are several handy functions for calculating features of the data that
brolgar provides. These all start with feat_, and include:
feat_ranges(): min, max, range difference, interquartile range;feat_spread(): variance, standard deviation, median absolute distance, and interquartile range;feat_monotonic(): is it always increasing, decreasing, or unvarying?;feat_diff_summary(): the summary statistics of the differences amongst a value, including the five number summary, as well as the standard deviation and variance;feat_brolgar(), which will calculate all features available in the brolgar package.- Other examples of features from the feasts package.
Feature sets
If you want to run many or all features from a package on your data you can collect them all with feature_set. For example:
library(fabletools)
feat_set_brolgar <- feature_set(pkgs = "brolgar")
length(feat_set_brolgar)[1] 6You could then run these like so:
# A tibble: 119 × 46
country min...1 med...2 max...3 min...4 q25...5 med...6 q75...7
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Afghanistan 161. 167. 168. 161. 164. 167. 168.
2 Algeria 166. 169 171. 166. 168. 169 170.
3 Angola 159. 167. 169. 159. 160. 167. 168.
4 Argentina 167. 168. 174. 167. 168. 168. 170.
5 Armenia 164. 169. 172. 164. 166. 169. 172.
6 Australia 170 172. 178. 170 171. 172. 173.
7 Austria 162. 167. 179. 162. 164. 167. 169.
8 Azerbaijan 170. 172. 172. 170. 171. 172. 172.
9 Bangladesh 160. 162. 164. 160. 162. 162. 163.
10 Belgium 163. 166. 177. 163. 164. 166. 168.
# … with 109 more rows, and 38 more variables: max...8 <dbl>,
# min...9 <dbl>, max...10 <dbl>, range_diff...11 <dbl>,
# iqr...12 <dbl>, var...13 <dbl>, sd...14 <dbl>, mad...15 <dbl>,
# iqr...16 <dbl>, min...17 <dbl>, max...18 <dbl>, median <dbl>,
# mean <dbl>, q25...21 <dbl>, q75...22 <dbl>, range1 <dbl>,
# range2 <dbl>, range_diff...25 <dbl>, sd...26 <dbl>,
# var...27 <dbl>, mad...28 <dbl>, iqr...29 <dbl>, …To see other features available in the feasts R package run library(feasts) then ?fabletools::feature_set.
Creating your own feature
To create your own features or summaries to pass to features, you provide a named vector of functions. These can include functions that you have written yourself. For example, returning the first three elements of a series, by writing our own second and third functions.
second <- function(x) nth(x, n = 2)
third <- function(x) nth(x, n = 3)
feat_first_three <- c(first = first,
second = second,
third = third)These are then passed to features like so:
# A tibble: 119 × 4
country first second third
<chr> <dbl> <dbl> <dbl>
1 Afghanistan 168. 166. 167.
2 Algeria 169. 166. 169
3 Angola 160. 159. 160.
4 Argentina 170. 168. 168
5 Armenia 169. 168. 166.
6 Australia 170 171. 170.
7 Austria 165. 163. 162.
8 Azerbaijan 170. 171. 171.
9 Bangladesh 162. 162. 164.
10 Belgium 163. 164. 164
# … with 109 more rowsAs well, brolgar provides some useful additional features for the five number summary, feat_five_num, whether keys are monotonically increasing feat_monotonic, and measures of spread or variation, feat_spread. Inside brolgar, the features are created with the following syntax:
feat_five_num <- function(x, ...) {
c(
min = b_min(x, ...),
q25 = b_q25(x, ...),
med = b_median(x, ...),
q75 = b_q75(x, ...),
max = b_max(x, ...)
)
}Here the functions b_ are functions with a default of na.rm = TRUE, and in
the cases of quantiles, they use type = 8, and names = FALSE. What is particularly useful is that these will work on any type of time series data, and you can use other more typical time series features from the feasts package, such as autocorrelation, feat_acf() and Seasonal and Trend decomposition using Loess feat_stl() (O’Hara-Wild et al. 2020b).
This demonstrates a workflow that can be used to understand and explore your longitudinal data. The brolgar package builds upon this workflow made available by feasts and fabletools. Users can also create their own features to summarise the data.
4 Breaking up the Spaghetti
Plots like Figure 2 are often called, “spaghetti plots”, and can be useful for a high level understanding as a whole. However, we cannot process and understand the individuals when the data is presented like this.
Sampling
Just how spaghetti is portioned out for consumption, we can sample some of the data by randomly sampling the data into sub-plots with the facet_sample() function (Figure 4).
ggplot(heights_brolgar,
aes(x = year,
y = height_cm,
group = country)) +
geom_line() +
facet_sample() +
scale_x_continuous(breaks = c(1750, 1850, 1950))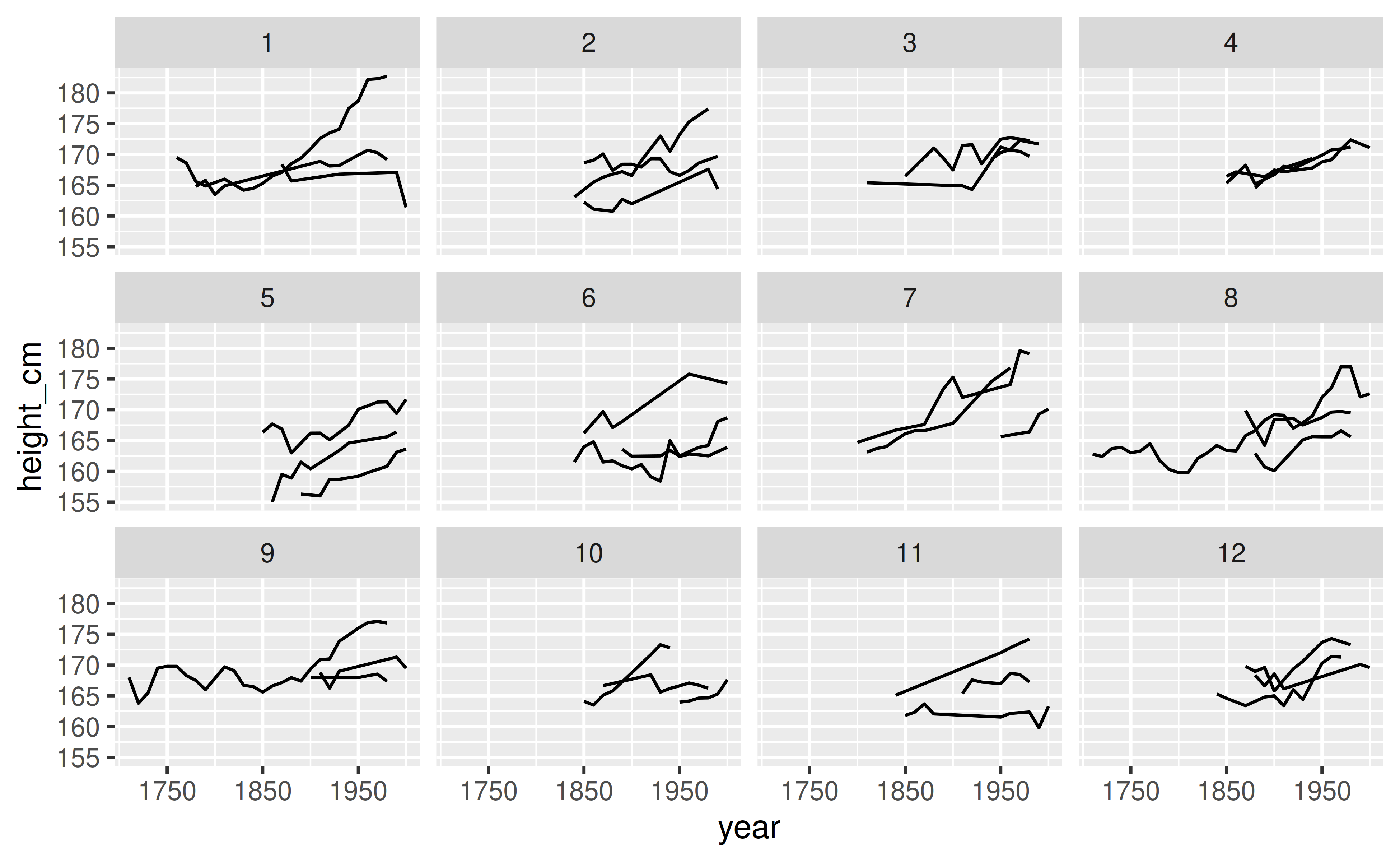
Figure 4: Twelve facets with three keys per facet shown. This allows us to quickly view a random sample of the data.
This defaults to 12 facets and 3 samples per facet, and provides options for the number of facets, and the number of samples per facet. This means the user only needs to consider the most relevant questions: “How many keys per facet?” and “How many facets to look at?”. The code to change the figure from Figure 2 into 4 requires only one line of code, shown below:
ggplot(heights_brolgar,
aes(x = year,
y = height_cm,
group = country)) +
geom_line() +
facet_sample()Stratifying
Extending this idea of samples, we can instead look at all of the data, spread out equally over facets, using facet_strata(). It uses 12 facets by default, controllable with n_strata. The code to do so is shown below, creating Figure 5.
ggplot(heights_brolgar,
aes(x = year,
y = height_cm,
group = country)) +
geom_line() +
facet_strata() +
scale_x_continuous(breaks = c(1750, 1850, 1950))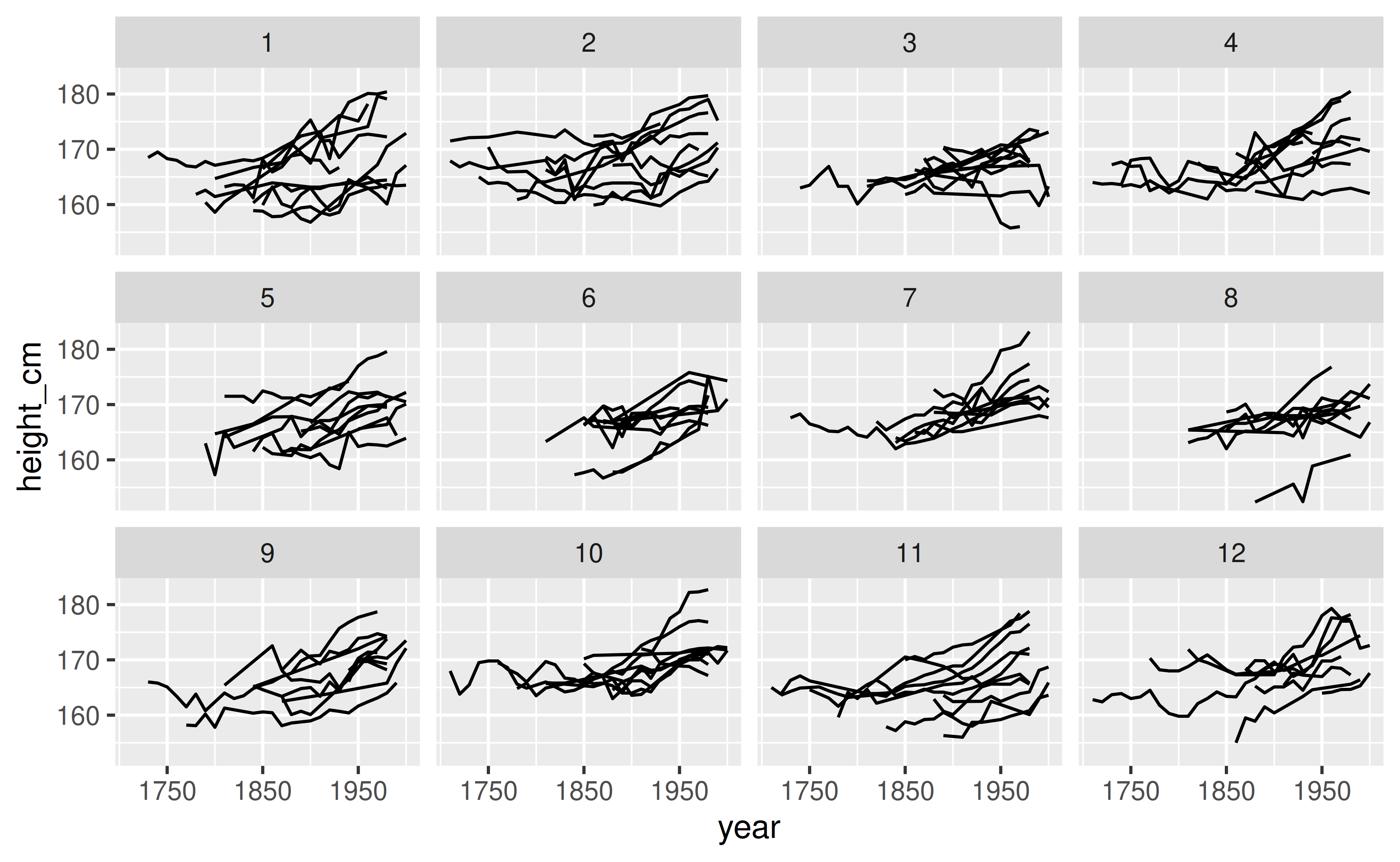
Figure 5: All of the data is shown by spreading out each key across twelve facets. Each key is only shown once, and is randomly allocated to a facet.
Featuring
Figure 4 and Figure 5 only show each key once, being randomly assigned to a facet. We can meaningfully place the keys into facets, by arranging the heights “along” a variable, like year, using the along argument in facet_strata to produce Figure 6:
ggplot(heights_brolgar,
aes(x = year,
y = height_cm,
group = country)) +
geom_line() +
facet_strata(along = -year) +
scale_x_continuous(breaks = c(1750, 1850, 1950))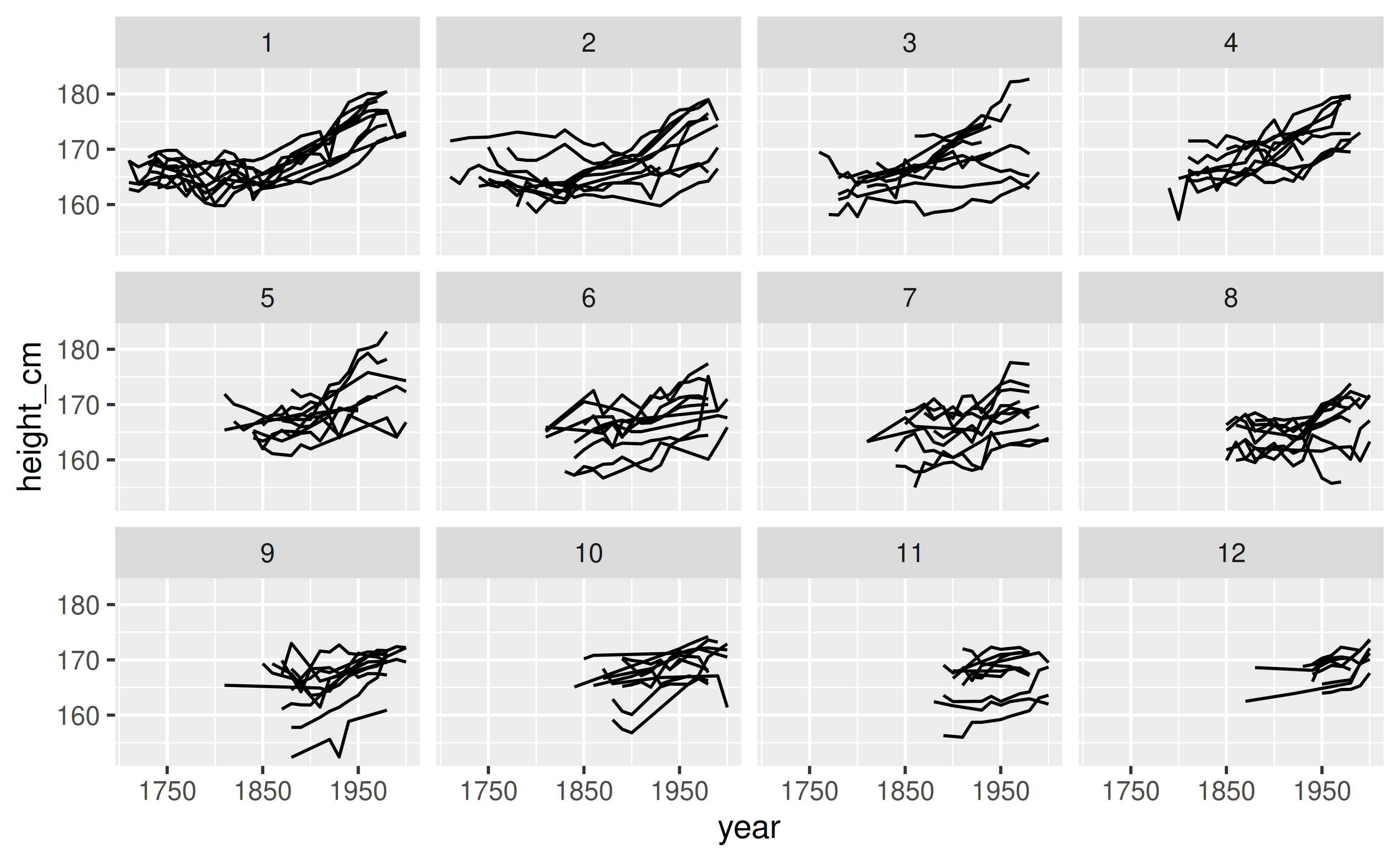
Figure 6: Displaying all the data across twelve facets. Instead of each key being randomly in a facet, each facet displays a specified range of values of year. In this case, the top left facet shows the keys with the earliest starting year, and the bottom right shows the facet with the latest starting year.
We have not lost any of the data, only the order in which they are presented has changed. We learn the distribution and changes in heights over time, and those measured from the earliest times appear to be more similar, but there is much wider variation in the middle years, and then for more recent heights measured from the early 1900s, the heights are more similar. The starting point of each of these years seems to increase at roughly the same interval. This informs us that the starting times of the years is approximately uniform.
Together facet_sample() and facet_strata() allow for rapid exploration, by focusing on relevant questions instead of the minutiae. This is achieved by appropriately randomly assigning while maintaining key structure, keeping the correct number of keys per plot, and so on. For example, facet_sample() the questions are: “How many lines per facet” and “How many facets?”, and for facet_strata() the questions are: “How many facets / strata?” and “What to arrange plots along?”.
Answering these questions keeps the analysis in line with the analytic goals of exploring the data, rather than distracting to minutiae. This is a key theme of improving tools for data analysis. Abstracting away the parts that are not needed, so the analyst can focus on the task at hand.
Under the hood, facet_sample() and facet_strata() are powered with sample_n_keys() and stratify_keys(). These can be used to create data structures used in facet_sample() and facet_strata(), and extend them for other purposes.
Using a tsibble stores important key and index components, in turn allowing for better ways to break up spaghetti plots so we can look at many and all sub-samples using facet_sample() and facet_strata().
5 Book-keeping
Longitudinal data is not always measured at the same time and at the same frequency. When exploring longitudinal data, a useful first step is to explore the frequency of measurements of the index. We can check if the index is regular using index_regular() and summarise the spacing of the index with index_summary(). These are S3 methods, so for data.frame objects, the index must be specified, however for the tsibble objects, the defined index is used.
index_summary(heights_brolgar) Min. 1st Qu. Median Mean 3rd Qu. Max.
1710 1782 1855 1855 1928 2000 index_regular(heights_brolgar)[1] TRUEWe can explore how many observations per country by counting the number of observations with features, like so:
# A tibble: 119 × 2
country n_obs
<chr> <int>
1 Afghanistan 5
2 Algeria 5
3 Angola 9
4 Argentina 20
5 Armenia 11
6 Australia 10
7 Austria 18
8 Azerbaijan 7
9 Bangladesh 9
10 Belgium 10
# … with 109 more rowsThis can be further summarised by counting the number of times there are a given number of observations:
# A tibble: 24 × 2
n_obs n
<int> <int>
1 5 11
2 6 11
3 7 13
4 8 5
5 9 12
6 10 12
7 11 9
8 12 4
9 13 7
10 14 6
# … with 14 more rowsBecause we are exploring the temporal patterns, we cannot reliably say anything about those individuals with few measurements. The data used, heights_brolgar has less than 5 measurements. This was done using add_n_obs(), which adds the number of observations to the existing data. Overall this drops 25 countries, leaves us with 119 out of the original 144 countries.
We can further explore when countries are first being measured using features to find the first year for each country number of starting years with the first function from dplyr, and explore this with a visualisation (Figure 7).
# A tibble: 119 × 2
country first
<chr> <dbl>
1 Afghanistan 1870
2 Algeria 1910
3 Angola 1790
4 Argentina 1770
5 Armenia 1850
6 Australia 1850
7 Austria 1750
8 Azerbaijan 1850
9 Bangladesh 1850
10 Belgium 1810
# … with 109 more rows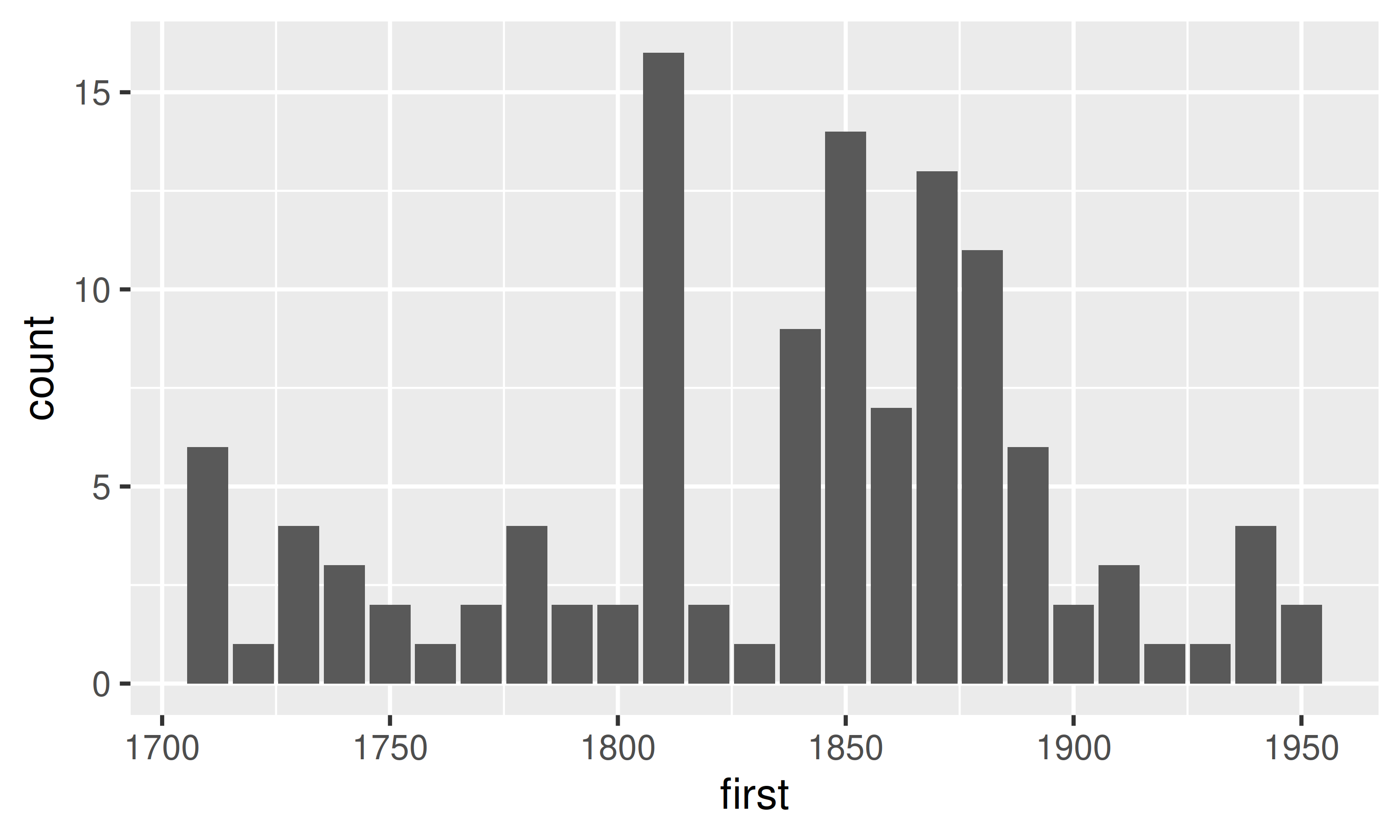
Figure 7: Distribution of starting years of measurement. The data is already binned into 10 year blocks. Most of the years start between 1840 and 1900.
We can explore the variation in first year using feat_diff_summary. This combines many summaries of the differences in year.
# A tibble: 119 × 10
country diff_…¹ diff_…² diff_…³ diff_…⁴ diff_…⁵ diff_…⁶ diff_…⁷
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Afghanistan 10 10 30 32.5 55.8 60 692.
2 Algeria 10 10 10 22.5 39.2 60 625
3 Angola 10 10 10 17.5 10 70 450
4 Argentina 10 10 10 11.6 10 40 47.4
5 Armenia 10 10 10 15 20.8 30 72.2
6 Australia 10 10 10 13.3 10 40 100
7 Austria 10 10 10 13.5 10 40 74.3
8 Azerbaijan 10 10 10 25 25.8 90 1030
9 Bangladesh 10 10 10 18.8 15.8 70 441.
10 Belgium 10 10 10 16.7 23.3 40 125
# … with 109 more rows, 2 more variables: diff_sd <dbl>,
# diff_iqr <dbl>, and abbreviated variable names ¹diff_min,
# ²diff_q25, ³diff_median, ⁴diff_mean, ⁵diff_q75, ⁶diff_max,
# ⁷diff_varThis is particularly useful as using diff on year would return a very wide dataset that is hard to explore:
# A tibble: 119 × 30
country ...1 ...2 ...3 ...4 ...5 ...6 ...7 ...8 ...9 ...10
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Afghan… 10 50 60 10 NA NA NA NA NA NA
2 Algeria 10 10 60 10 NA NA NA NA NA NA
3 Angola 10 10 70 10 10 10 10 10 NA NA
4 Argent… 10 10 10 10 10 10 10 10 10 10
5 Armenia 10 30 10 10 30 20 10 10 10 10
6 Austra… 10 10 10 10 10 10 10 40 10 NA
7 Austria 20 10 10 30 10 10 10 10 10 10
8 Azerba… 10 90 10 10 10 20 NA NA NA NA
9 Bangla… 10 10 10 70 10 20 10 10 NA NA
10 Belgium 10 10 10 10 10 10 30 40 20 NA
# … with 109 more rows, and 19 more variables: ...11 <dbl>,
# ...12 <dbl>, ...13 <dbl>, ...14 <dbl>, ...15 <dbl>, ...16 <dbl>,
# ...17 <dbl>, ...18 <dbl>, ...19 <dbl>, ...20 <dbl>, ...21 <dbl>,
# ...22 <dbl>, ...23 <dbl>, ...24 <dbl>, ...25 <dbl>, ...26 <dbl>,
# ...27 <dbl>, ...28 <dbl>, ...29 <dbl>We can then look at the summaries of the differences in year by changing to long form and facetting (Figure 8), we learn about the range of intervals between measurements, the smallest being 10 years, the largest being 125, and that most of the data is measured between 10 and 30 years.
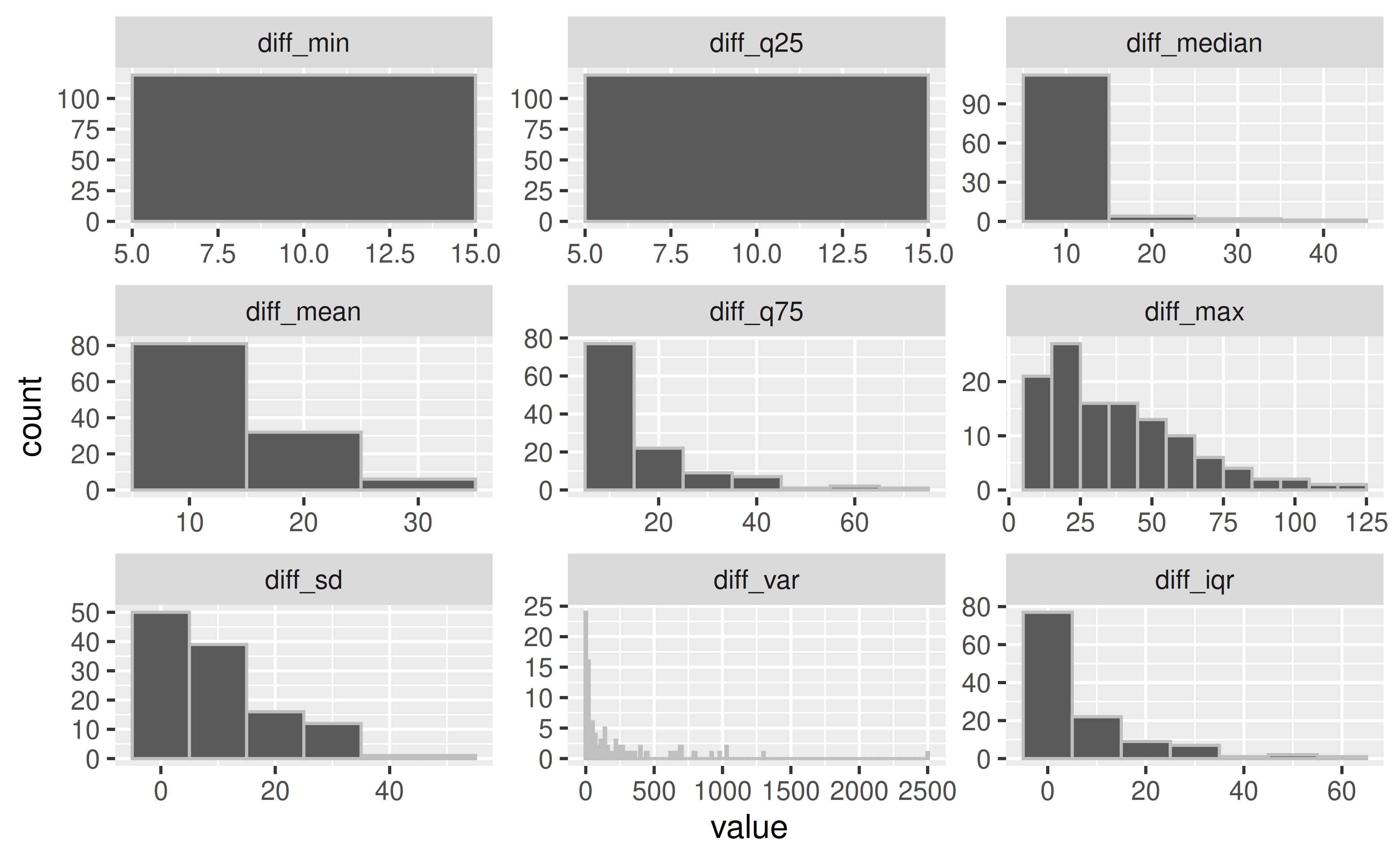
Figure 8: Exploring the different summary statistics of the differences amongst the years. We learn that the smallest interval between measurements is 10 years, and the largest interval is between 10 and 125 years, and that most of the data is measured between 10 and 30 or so years.
6 Finding Waldo
Looking at a spaghetti plot, it can be hard to identify which lines are the most interesting, or unusual. A workflow to identify interesting individuals to start with is given below:
- Decide upon an interesting feature (e.g., maximum)
- This feature produces one value per key
- Examine the distribution of the feature
- Join this table back to the data to get all observations for those keys
- Arrange the keys or filter, using the feature
- Display the data for selected keys
This workflow is now demonstrated. Firstly, we decide on an interesting feature, “maximum height”, and whether height is always increasing. We calculate our own “feature”, calculating maximum height, and whether a value is increasing (with brolgar’s increasing function) as follows:
heights_max_in <- heights_brolgar %>%
features(height_cm, list(max = max,
increase = increasing))
heights_max_in# A tibble: 119 × 3
country max increase
<chr> <dbl> <lgl>
1 Afghanistan 168. FALSE
2 Algeria 171. FALSE
3 Angola 169. FALSE
4 Argentina 174. FALSE
5 Armenia 172. FALSE
6 Australia 178. FALSE
7 Austria 179. FALSE
8 Azerbaijan 172. FALSE
9 Bangladesh 164. FALSE
10 Belgium 177. FALSE
# … with 109 more rowsThis returns a dataset of one value per key. Figure 9 examines the distribution of the features, showing us the distribution of maximum height, and the number of countries that are always increasing.
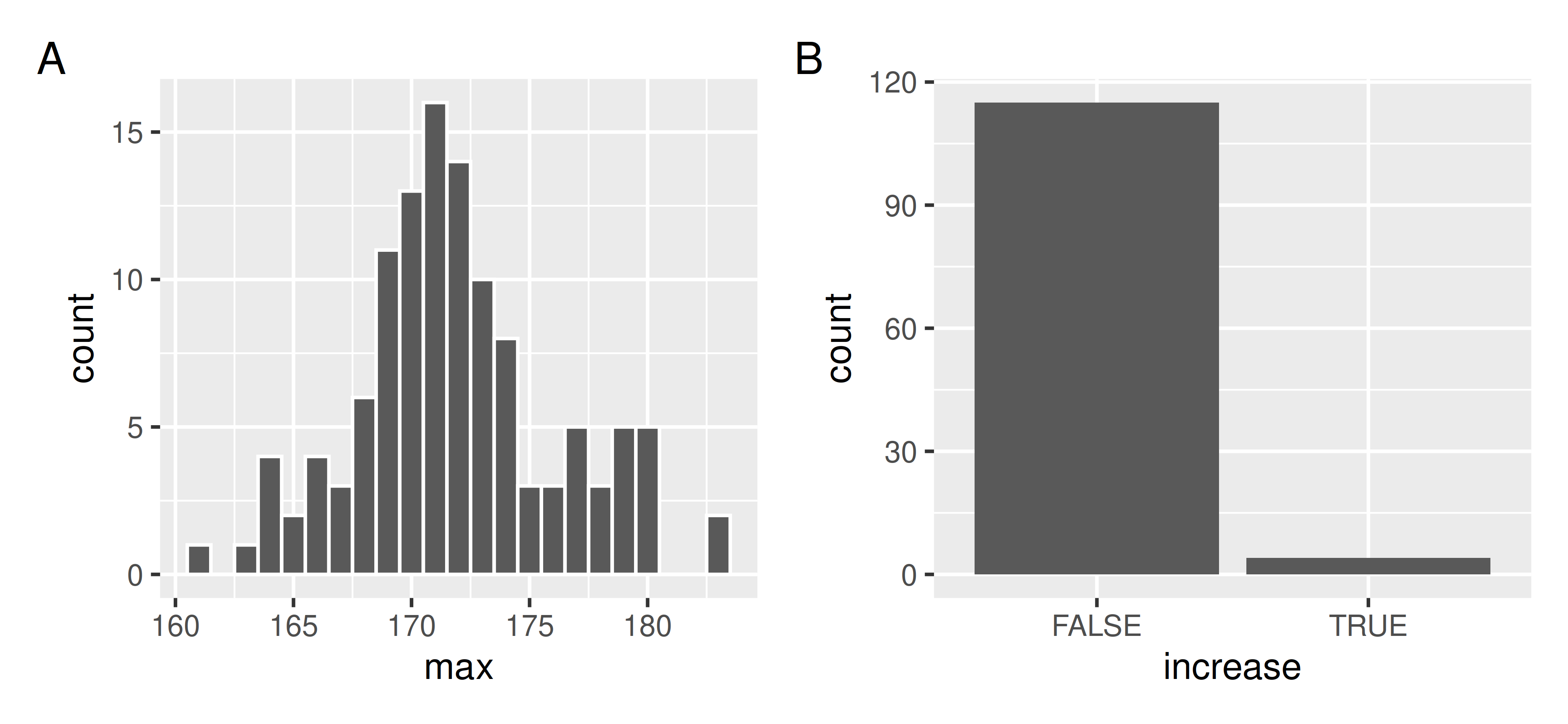
Figure 9: The different distributions of the features - A is depicting the distribution of maximum height, and B displays the number of countries that are always increasing (FALSE), and always increasing (TRUE). We note that the average maximum heights range from about 160cm to 185cm, with most being around 170cm. We also learn that the vast majority of countries are not always increasing in height through time.
We can now join this table back to the data to get all observations for those keys to move from one key per row to all many rows per key.
heights_max_in_full <- heights_max_in %>%
left_join(heights_brolgar,
by = "country")
heights_max_in_full# A tibble: 1,406 × 9
country max incre…¹ year n_obs conti…² heigh…³ year0 count…⁴
<chr> <dbl> <lgl> <dbl> <int> <chr> <dbl> <dbl> <fct>
1 Afghanistan 168. FALSE 1870 5 Asia 168. 160 Afghan…
2 Afghanistan 168. FALSE 1880 5 Asia 166. 170 Afghan…
3 Afghanistan 168. FALSE 1930 5 Asia 167. 220 Afghan…
4 Afghanistan 168. FALSE 1990 5 Asia 167. 280 Afghan…
5 Afghanistan 168. FALSE 2000 5 Asia 161. 290 Afghan…
6 Algeria 171. FALSE 1910 5 Africa 169. 200 Algeria
7 Algeria 171. FALSE 1920 5 Africa 166. 210 Algeria
8 Algeria 171. FALSE 1930 5 Africa 169 220 Algeria
9 Algeria 171. FALSE 1990 5 Africa 171. 280 Algeria
10 Algeria 171. FALSE 2000 5 Africa 170. 290 Algeria
# … with 1,396 more rows, and abbreviated variable names ¹increase,
# ²continent, ³height_cm, ⁴country_fctWe can then arrange the keys or filter, using the feature, for example, filtering only those countries that are only increasing:
# A tibble: 22 × 9
country max increase year n_obs continent heigh…¹ year0 count…²
<chr> <dbl> <lgl> <dbl> <int> <chr> <dbl> <dbl> <fct>
1 Honduras 168. TRUE 1950 6 Americas 164. 240 Hondur…
2 Honduras 168. TRUE 1960 6 Americas 164. 250 Hondur…
3 Honduras 168. TRUE 1970 6 Americas 165. 260 Hondur…
4 Honduras 168. TRUE 1980 6 Americas 165. 270 Hondur…
5 Honduras 168. TRUE 1990 6 Americas 165. 280 Hondur…
6 Honduras 168. TRUE 2000 6 Americas 168. 290 Hondur…
7 Moldova 174. TRUE 1840 5 Europe 165. 130 Moldova
8 Moldova 174. TRUE 1950 5 Europe 172. 240 Moldova
9 Moldova 174. TRUE 1960 5 Europe 173. 250 Moldova
10 Moldova 174. TRUE 1970 5 Europe 174. 260 Moldova
# … with 12 more rows, and abbreviated variable names ¹height_cm,
# ²country_fctOr tallest country
heights_top <- heights_max_in_full %>% top_n(n = 1, wt = max)
heights_top# A tibble: 16 × 9
country max increase year n_obs continent height…¹ year0 count…²
<chr> <dbl> <lgl> <dbl> <int> <chr> <dbl> <dbl> <fct>
1 Denmark 183. FALSE 1820 16 Europe 167. 110 Denmark
2 Denmark 183. FALSE 1830 16 Europe 165. 120 Denmark
3 Denmark 183. FALSE 1850 16 Europe 167. 140 Denmark
4 Denmark 183. FALSE 1860 16 Europe 168. 150 Denmark
5 Denmark 183. FALSE 1870 16 Europe 168. 160 Denmark
6 Denmark 183. FALSE 1880 16 Europe 170. 170 Denmark
7 Denmark 183. FALSE 1890 16 Europe 169. 180 Denmark
8 Denmark 183. FALSE 1900 16 Europe 170. 190 Denmark
9 Denmark 183. FALSE 1910 16 Europe 170 200 Denmark
10 Denmark 183. FALSE 1920 16 Europe 174. 210 Denmark
11 Denmark 183. FALSE 1930 16 Europe 174. 220 Denmark
12 Denmark 183. FALSE 1940 16 Europe 176. 230 Denmark
13 Denmark 183. FALSE 1950 16 Europe 180. 240 Denmark
14 Denmark 183. FALSE 1960 16 Europe 180. 250 Denmark
15 Denmark 183. FALSE 1970 16 Europe 181. 260 Denmark
16 Denmark 183. FALSE 1980 16 Europe 183. 270 Denmark
# … with abbreviated variable names ¹height_cm, ²country_fctWe can then display the data by highlighting it in the background, first creating a background plot and overlaying the plots on top of this as an additional ggplot layer, in Figure 10.
Figure 10: Interactive plot to explore longnostics of maximum height and slope from a simple linear fit, relative to the profiles. Click on either plot to select countries. For example, the country with the most negative slope, that is people are getting shorter is Eritrea.
7 Dancing with Models
These same workflows can be used to interpret and explore a model. As the data tends to follow a non linear trajectory, we use a general additive model (gam) with the mgcv R package (Wood 2017) using the code below:
heights_gam <- gam(
height_cm ~ s(year0, by = country_fct) + country_fct,
data = heights_brolgar,
method = "REML"
)This fits height in centimetres with a smooth effect for year for each country, with a different intercept for each country. It is roughly equivalent to a random intercept varying slope model. Note that this gam model took approximately 8074 seconds to fit. We add the predicted and residual values for the model below, as well as the residual sums of squares for each country.
We can use the previous approach to explore the model results. We can take a look at a sample of the predictions along with the data, by using sample_n_keys. This provides a useful way to explore some set of the model predictions. In order to find those predictions that best summarise the best, and worst, and in between, we need to use the methods in the next section, “Stereotyping”.
heights_aug %>%
sample_n_keys(12) %>%
ggplot(aes(x = year,
y = pred,
group = country)) +
geom_line(colour = "steelblue") +
geom_point(aes(y = height_cm)) +
facet_wrap(~country)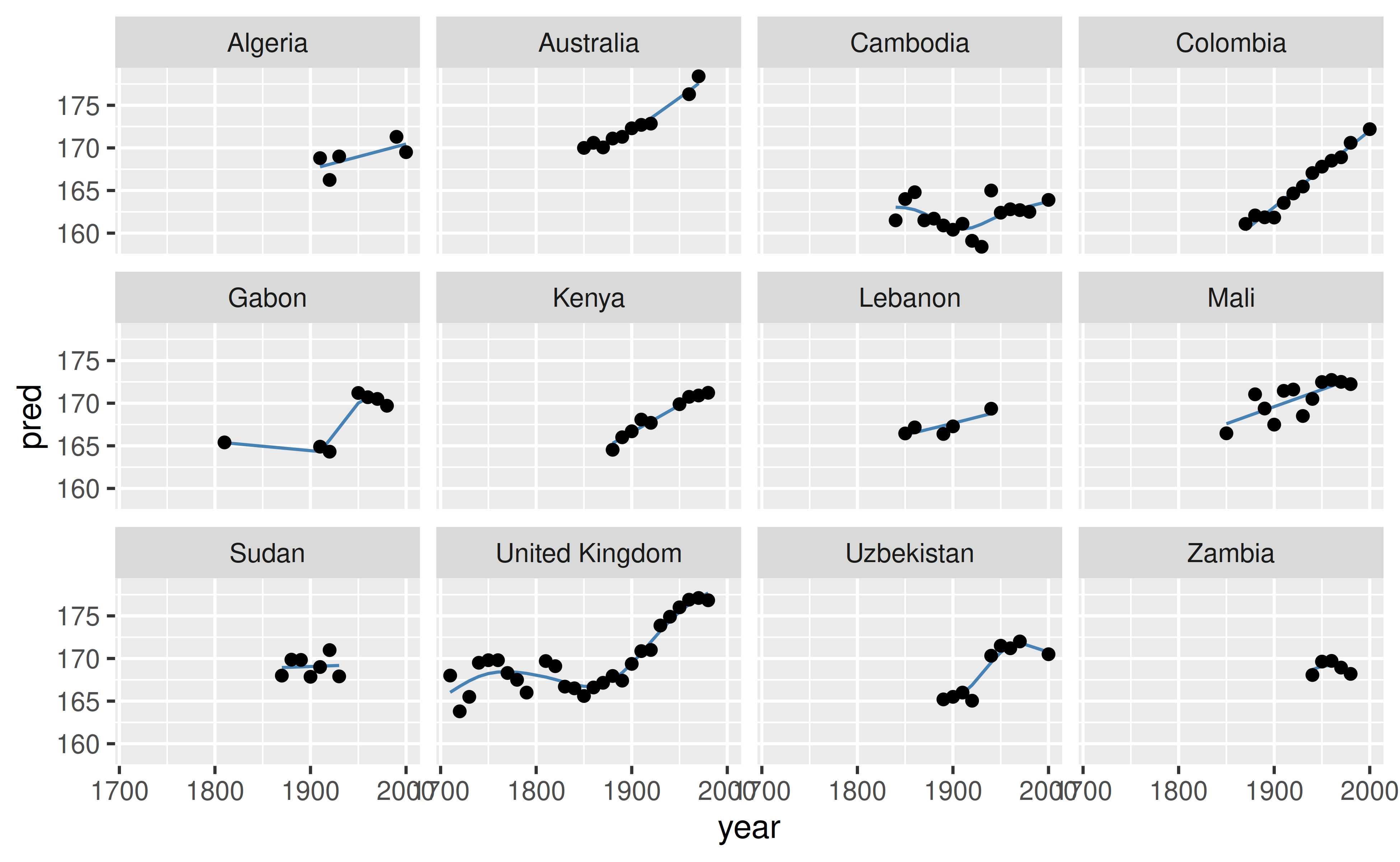
Figure 11: Exploration of a random sample of the data. This shows the data points of 12 countries, with the model fit in blue.
8 Stereotyping
To help understand a population of measurements over time, it can be useful to understand which individual measurements are typical (or “stereotypical”) of a measurement. For example, to understand which individuals are stereotypical of a statistic such as the minimum, median, and maximum height. This section discusses how to find these stereotypes in the data.
Figure 12 shows the residuals of the simple model fit to the data in the previous section. There is an overlaid five number summary, showing the minimum, 1st quantile, median, 3rd quantile, and maximum residual value residuals, as well as a rug plot to show the data. We can use these residuals to understand the stereotypes of the data - those individuals in the model that best match to this five number summary.
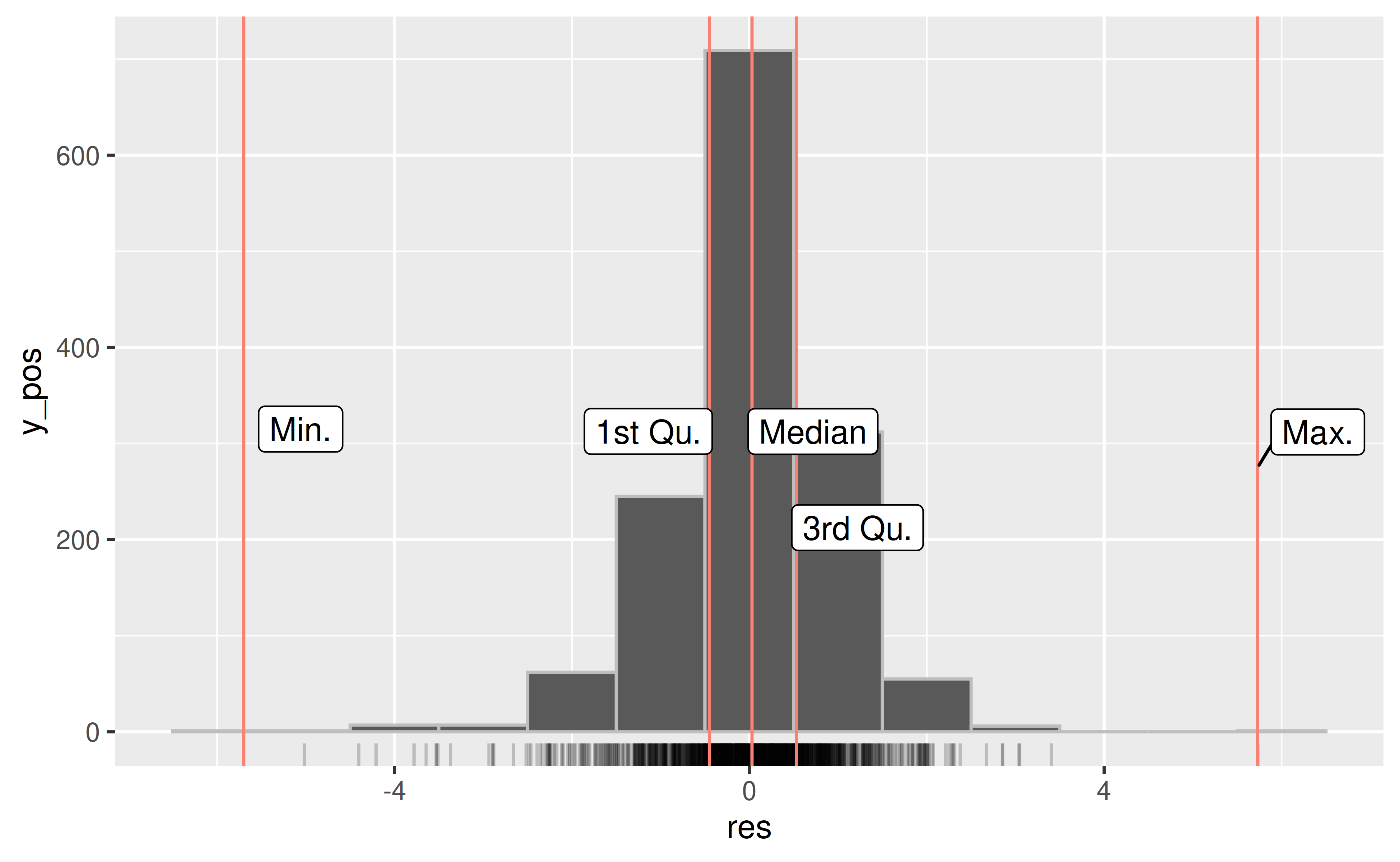
Figure 12: Five number summary of residual values from the model fit. The residuals are centered around zero with some variation.
We can do this using keys_near() from brolgar. By default this uses the 5 number summary, but any function can be used. You specify the variable you want to find the keys nearest, in this case rss, residual sums of squares for each key:
keys_near(heights_aug, var = rss)# A tibble: 62 × 5
country rss stat stat_value stat_diff
<chr> <dbl> <fct> <dbl> <dbl>
1 Denmark 9.54 med 9.54 0
2 Denmark 9.54 med 9.54 0
3 Denmark 9.54 med 9.54 0
4 Denmark 9.54 med 9.54 0
5 Denmark 9.54 med 9.54 0
6 Denmark 9.54 med 9.54 0
7 Denmark 9.54 med 9.54 0
8 Denmark 9.54 med 9.54 0
9 Denmark 9.54 med 9.54 0
10 Denmark 9.54 med 9.54 0
# … with 52 more rowsTo plot the data, they need to be joined back to the original data, we use a left join, joining by country.
Figure 13 shows those countries closest to the five number summary. Observing this, we see that the minimum RSS for Moldova fits a nearly perfectly straight line, and the maximum residuals for Myanmar have wide spread of values.
ggplot(heights_near_aug,
aes(x = year,
y = pred,
group = country,
colour = country)) +
geom_line(colour = "orange") +
geom_point(aes(y = height_cm)) +
scale_x_continuous(breaks = c(1780, 1880, 1980)) +
facet_wrap(~stat + country,
labeller = label_glue("Country: {country} \nNearest to \n{stat} RSS"),
nrow = 1) +
theme(legend.position = "none",
aspect.ratio = 1)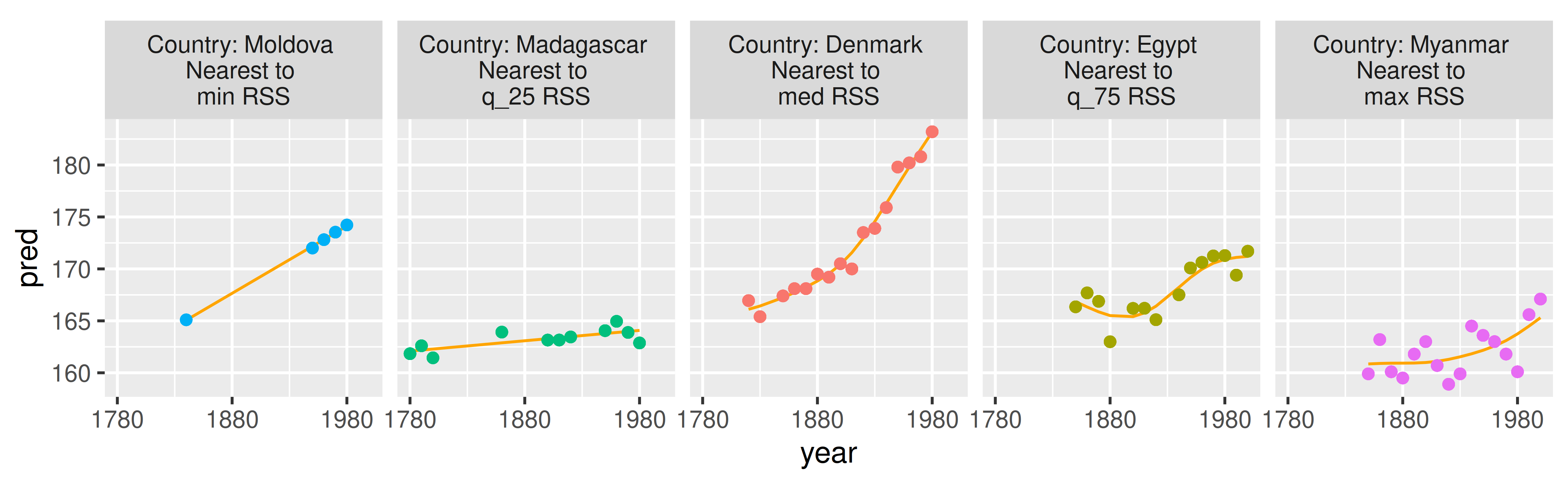
Figure 13: The keys nearest to the five number summary of the residual sums of squares. Moldova and Madagascar are well fit by the model, and are fit by a straight line. The remaining countries with poorer fit have greater variation in height. It is not clear how a better model fit could be achieved.
We can also look at the highest and lowest 3 residual sums of squares:
heights_near_aug_top_3 <- heights_aug %>%
distinct(country, rss) %>%
top_n(n = 3,
wt = rss)
heights_near_aug_bottom_3 <- heights_aug %>%
distinct(country, rss) %>%
top_n(n = -3,
wt = rss)
heights_near_top_bot_3 <- bind_rows(highest_3 = heights_near_aug_top_3,
lowest_3 = heights_near_aug_bottom_3,
.id = "rank") %>%
left_join(heights_aug,
by = c("country", "rss"))Figure 14 shows the same information as the previous plot, but with the 3 representative countries for each statistic. This gives us more data on what the stereotypically “good” and “poor” fitting countries to this model.
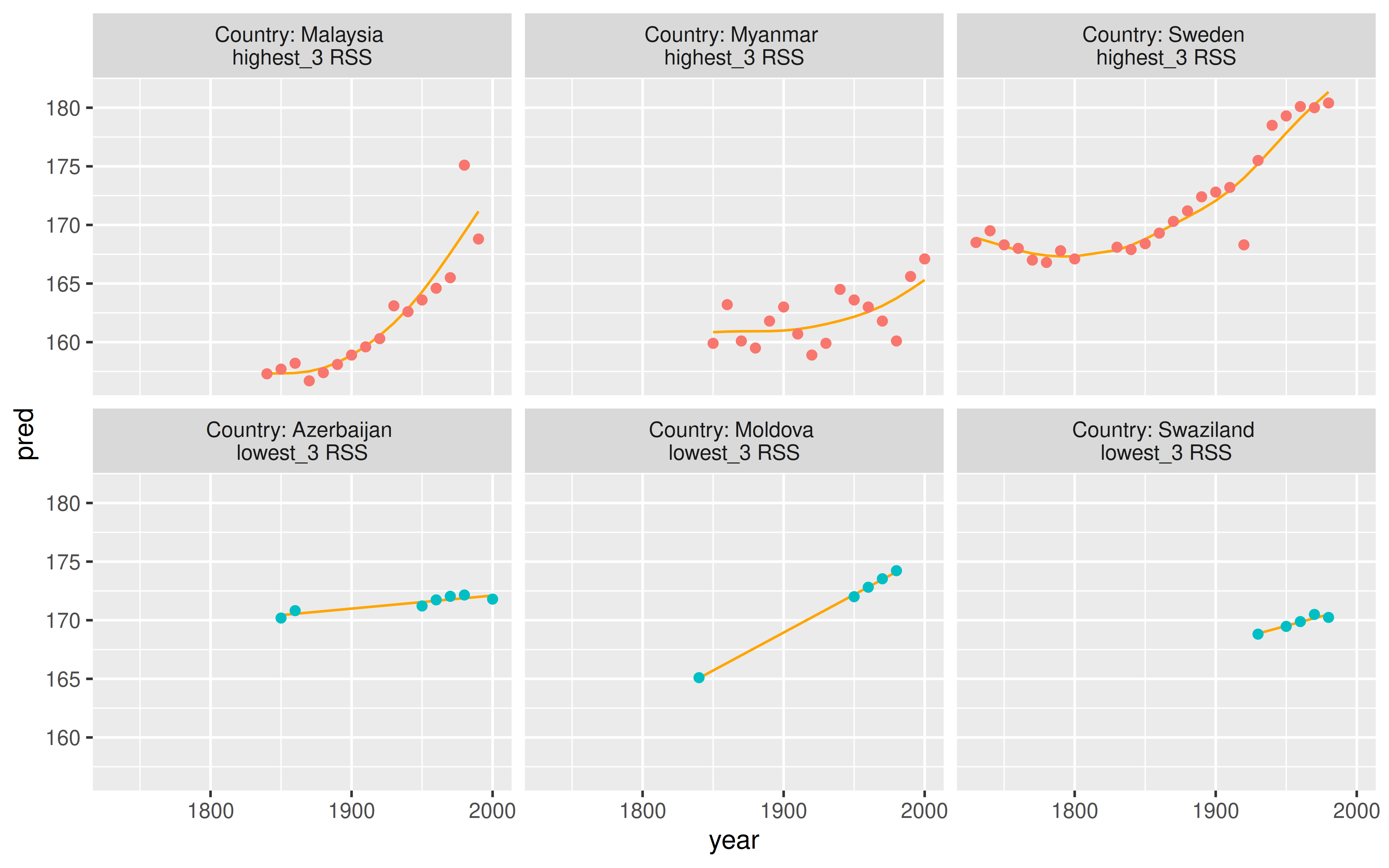
Figure 14: Figure of stereotypes for those keys with the three highest and lowest RSS values. Those that fit best tend to be linear, but those that fit worst have wider variation in heights.
9 Getting Started
The brolgar R package can be installed from CRAN using
# From CRAN
install.packages("brolgar")
# Development version
remotes::install_github("njtierney/brolgar")The functions are all designed to build upon existing packages, but are predicated on working with tsibble. The package extends upon ggplot2 to provide facets for exploration: facet_sample() and facet_strata(). Extending dplyr’s sample_n() and sample_frac() functions by providing sampling and stratifying based around keys: sample_n_keys(), sample_frac_keys(), and stratify_keys(). New functions are focussed around the use of key, for example key_slope() to find the slope of each key, and keys_near() to find those keys near a summary statistic. Finally, feature calculation is provided by building upon the existing time series feature package, feasts.
To get started with brolgar you must first ensure your data is specified as a tsibble - discussed earlier in the paper, there is also a vignette “Longitudinal Data Structures”, which discusses these ideas. The next step we recommend is sampling some of your data with facet_sample(), and facet_strata(). When using facet_strata(), facets can be arranged in order of a variable, using the along argument, which can reveal interesting features.
To further explore longitudinal data, we recommend finding summary features of each variable with features, and identifying variables that are near summary statistics, using keys_near to find individuals stereotypical of a statistical value.
10 Concluding Remarks
The brolgar package facilitates exploring longitudinal data in R. It builds upon existing infrastructure from tsibble, and feasts, which work within the tidyverse family of R packages, as well as the newer, tidyverts, time series packages. Users familiar with either of these package families will find a lot of similarity in their use, and first time users will be able to easily transition from brolgar to the tidyverse or tidyverts.
Visualizing categorical or binary data over a time period can be difficult as the limited number of values on the y axis leads to overplotting. This can conceal the number of values present at a given value. The tools discussed in brolgar facilitate this in the form of facet_sample, and facet_strata. Some special methods could be developed to add jitter or noise around these values on the y axis, while still maintaining the graphical axis and tick marks.
Future work will explore more features and stratifications, and stereotypes, and generalise the tools to work for data without time components, and other data types.
11 Acknowledgements
We would like to thank Stuart Lee, Mitchell O’Hara Wild, Earo Wang, and Miles McBain for their discussion on the design of brolgar. We would also like to thank Rob Hyndman, Monash University and ACEMS for their support of this research.
12 Paper Source
The complete source files for the paper can be found at https://github.com/njtierney/rjournal-brolgar. The paper is built using rmarkdown, targets and capsule to ensure R package versions are the same. See the README file on the github repository for details on recreating the paper.
Supplementary materials
Supplementary materials are available in addition to this article. It can be downloaded at RJ-2022-023.zip
CRAN packages used
brolgar, ts, xts, zoo, pmdplyr, dplyr, panelr, plm, tsibble, fable, feasts, fabletools, mgcv, ggplot2, targets, capsule
CRAN Task Views implied by cited packages
Bayesian, CausalInference, Databases, Econometrics, Environmetrics, Epidemiology, Finance, HighPerformanceComputing, MissingData, MixedModels, ModelDeployment, Phylogenetics, ReproducibleResearch, Spatial, SpatioTemporal, TeachingStatistics, TimeSeries